Back
BackProblem 3b
Calculate the speed of longitudinal waves in granite, using Tables in Chapters 12 and 13.
Problem 7
A 0.40-kg cord is stretched between two supports 8.7 m apart. When one support is struck by a hammer, a transverse wave travels down the cord and reaches the other support in 0.85 s. What is the tension in the cord?
Problem 8
A sailor strikes the side of his ship just below the surface of the sea. He hears the echo of the wave reflected from the ocean floor directly below 2.4 s later. How deep is the ocean at this point? (Use Tables 12–1 and 13–1.)
Problem 9b
A ski gondola [pronounced gon–do–la] is connected to the top of a hill by a steel cable of length 710 m and diameter 1.5 cm. As the gondola comes to the end of its run, it bumps into the terminal and sends a transverse wave pulse along the cable. It is observed that it took 17 s for the pulse to return. What is the tension in the cable?
Problem 16
Two earthquake waves of the same frequency travel through the same portion of the Earth, but one is carrying 3.5 times the energy. What is the ratio of the amplitudes of the two waves?
Problem 17a
What is the ratio of the intensities, of an earthquake P wave passing through the Earth and detected at two points 15 km and 55 km from the source?
Problem 26a
Consider the point x = 1.00 m on the cord of Example 15–6. Determine the maximum acceleration of this point.
Problem 27b
A transverse wave pulse travels to the right along a string with a speed v = 2.0 m/s. At the shape of the pulse is given by the function D = 0.45 cos (2.6x + 1.2), where D and x are in meters. Determine a formula for the wave pulse at any time t assuming there are no frictional losses.
Problem 28
A transverse wave with a frequency of 220 Hz and a wavelength of 10.0 cm is traveling along a cord. The maximum speed of particles on the cord is 0.10 the wave speed. What is the amplitude of the wave?
Problem 29a
A 572-Hz longitudinal wave in air has a speed of 345 m/s. What is the wavelength?
Problem 29b
A 572-Hz longitudinal wave in air has a speed of 345 m/s. How much time is required for the phase to change by 90° at a given point in space?
Problem 29c
A 572-Hz longitudinal wave in air has a speed of 345 m/s. At a particular instant, what is the phase difference (in degrees) between two points 4.4 cm apart?
Problem 30
Write the equation for the wave in Problem 29 traveling to the right, if its amplitude is 0.020 cm, and D = - 0.020 cm, at t = 0 and x = 0.
Problem 32b
A transverse wave on a cord is given by D(x,t) = 0.12 sin (3.0x - 15.0t), where D and x are in meters and t is in seconds. At t = 0.20s, what are the displacement, velocity, and acceleration of a point on the cord where x = 0.60 m?
Problem 44b
Suppose two linear waves of equal amplitude and frequency have a phase difference ϕ as they travel in the same medium. They can be represented by: D₁ = A sin (kx - ωt); D₂ = A sin ( kx - ωt + ϕ). What is the amplitude of this resultant wave? Is the wave purely sinusoidal, or not?
Problem 44d
Suppose two linear waves of equal amplitude and frequency have a phase difference ϕ as they travel in the same medium. They can be represented by: D₁ = A sin (kx - ωt); D₂ = A sin ( kx - ωt + ϕ). Describe the resultant wave, by equation and in words, if ϕ = π/2.
Problem 47
A particular string resonates in four loops at a frequency of 320 Hz. Name at least three other frequencies at which it will resonate. What is each called?
Problem 50
The speed of waves on a string is 96 m/s. If the frequency of standing waves is 435 Hz, how far apart are two adjacent nodes?
Problem 52
A guitar string is 91 cm long and has a mass of 3.2 g. The vibrating portion of the string from the bridge to the support post is ℓ = 64cm and the string is under a tension of 520 N. What are the frequencies of the fundamental and first two overtones?
Problem 53c
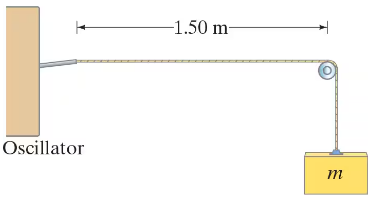
One end of a horizontal string is attached to a small-amplitude mechanical 60.0-Hz oscillator. The string’s mass per unit length is 3.9 x 10⁻ ⁴ kg/m. The string passes over a pulley, a distance ℓ = 1.50 m away, and weights are hung from this end, Fig. 15–38. What mass m must be hung from this end of the string to produce five loops of a standing wave? Assume the string at the oscillator is a node, which is nearly true.
Problem 55a
The displacement of a standing wave on a string is given by D = 2.4 sin ( 0.60x ) cos (42t) , where x and D are in centimeters and t is in seconds. What is the distance (cm) between nodes?
Problem 55b
The displacement of a standing wave on a string is given by D = 2.4sin(0.60x)cos(42t), where x and D are in centimeters and t is in seconds. Give the amplitude, frequency, and speed of each of the component waves.
Problem 57
A particular violin string plays at a frequency of 294 Hz. If the tension is increased 22%, what will the new frequency be?
Problem 60a
A standing wave on a 1.85-m-long horizontal string displays three loops when the string vibrates at 125 Hz. The maximum swing of the string (top to bottom) at the center of each loop is 8.00 cm. What is the function describing the standing wave?
Problem 63
When you slosh the water back and forth in a tub at just the right frequency, the water alternately rises and falls at each end, remaining relatively calm at the center. Suppose the frequency to produce such a standing wave in a 45-cm-wide tub is 0.85 Hz. What is the speed of the water wave?
Problem 66a
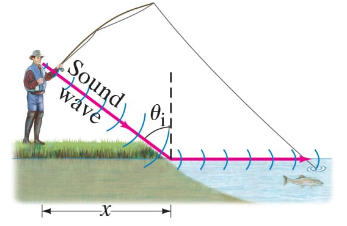
(II) For any type of wave that reaches a boundary beyond which its speed is increased, there is a maximum incident angle if there is to be a transmitted refracted wave. This maximum incident angle θiM corresponds to an angle of refraction equal to 90°. If θᵢ > θiM, all the wave is reflected at the boundary and none is refracted, because this would correspond to sin θᵣ > 1 (where is the angle θᵣ of refraction), which is impossible.
(a) Find a formula for θiM using the law of refraction, Eq. 15–19.
Problem 68
A longitudinal earthquake wave strikes a boundary between two types of rock at a 41° angle. As the wave crosses the boundary, the specific gravity of the rock changes from 3.6 to 2.8. Assuming that the elastic modulus (Section 15–2)is the same for both types of rock, determine the angle of refraction.
Problem 72
A guitar string is supposed to vibrate at 247 Hz, but is measured to actually vibrate at 262 Hz. By what percentage should the tension in the string be changed to get the frequency to the correct value?
Problem 75b
A bug on the surface of a pond is observed to move up and down a total vertical distance of 0.10 m, lowest to highest point, as a wave passes. If the amplitude increases to 0.15 m, by what factor does the bug’s maximum kinetic energy change?
Problem 76
Destructive interference occurs where two overlapping waves are 1/2 wavelength or 180° out of phase. Explain why 180° is equivalent to 1/2 wavelength.