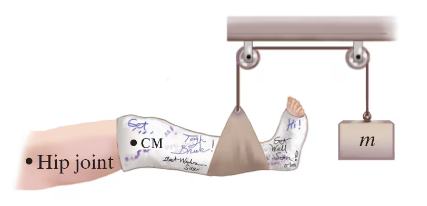
Calculate the mass m needed in order to suspend the leg shown in Fig. 12–50. Assume the leg (with cast) has a mass of 15.0 kg, and its cg is 35.0 cm from the hip joint; the cord holding the sling is 78.0 cm from the hip joint.

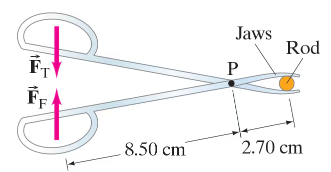
Figure 12–53 shows a pair of forceps used to hold a thin plastic rod firmly. If the thumb and finger each squeeze with a force F_T = F_F = 11.0 N, what force do the forceps jaws exert on the plastic rod?

(II) The force required to pull the cork out of the top of a wine bottle is in the range of 200 to 400 N. What range of forces F is required to open a wine bottle with the bottle opener shown in Fig. 12–58?

<IMAGE>

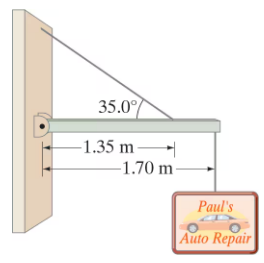
A shop sign weighing 215 N hangs from the end of a uniform 135-N beam as shown in Fig. 12–59. Find the tension in the supporting wire (at 35.0°), and the horizontal and vertical forces exerted by the hinge on the beam at the wall.

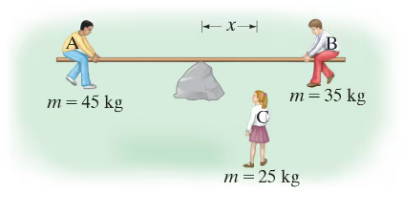
Three children are trying to balance on a seesaw, which includes a fulcrum rock acting as a pivot at the center, and a very light board 3.2 m long (Fig. 12–60). Two playmates are already on either end. Boy A has a mass of 45 kg, and boy B a mass of 35 kg. Where should girl C, whose mass is 25 kg, place herself so as to balance the seesaw?

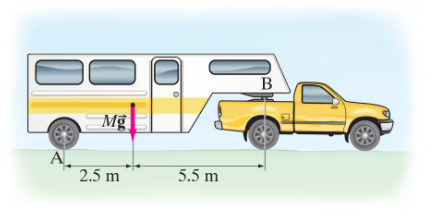
A 2300-kg trailer is attached to a stationary truck at point B, Fig. 12–64. Determine the normal force exerted by the road on the rear tires at A, and the vertical force exerted on the trailer by the support B.

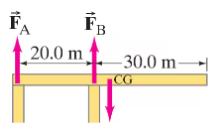
A 172-cm-tall person lies on a light (massless) board which is supported by two scales, one under the top of her head and one beneath the bottom of her feet (Fig. 12–65). The two scales read, respectively, 35.1 and 31.6 kg. What distance is the center of gravity of this person from the top of her head?

<IMAGE>

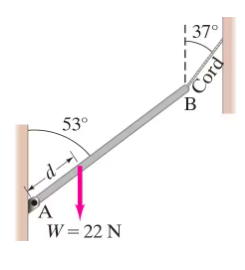
A uniform rod AB of length 4.5 m and mass M = 3.8 kg is hinged at A and held in equilibrium by a light cord, as shown in Fig. 12–69. A load W = 22 N hangs from the rod at a distance d so that the tension in the cord is 85 N. Draw a free-body diagram for the rod.

A refrigerator is approximately a uniform rectangular solid 1.9 m tall, 1.0 m wide, and 0.75 m deep. If it sits upright on a truck with its 1.0-m dimension in the direction of travel, and if the refrigerator cannot slide on the truck, how rapidly can the truck accelerate without tipping the refrigerator over? [Hint: The normal force would act at one corner.]

The Leaning Tower of Pisa is 55 m tall and about 7.7 m in radius. The top is 4.5 m off center. Is the tower in stable equilibrium? If so, how much farther can it lean before it becomes unstable? Assume the tower is of uniform composition.

A marble column of cross-sectional area 1.4m² supports a mass of 22,000 kg. By how much is the column shortened if it is 8.6 m high?

A 15-cm-long tendon was found to stretch 3.7 mm by a force of 13.4 N. The tendon was approximately round with an average diameter of 8.5 mm. Calculate Young’s modulus of this tendon.

Assume the supports of the uniform cantilever shown in Fig. 12–79 (m = 2900 kg) are made of wood. Calculate the minimum cross-sectional area required of each, assuming a safety factor of 9.0.

A steel cable is to support an elevator whose total (loaded) mass is not to exceed 3100 kg. If the maximum acceleration of the elevator is 1.8 m/s² , calculate the diameter of cable required. Assume a safety factor of 8.0.

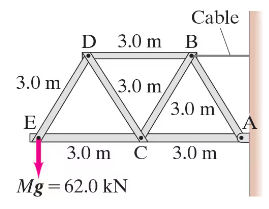
A heavy load Mg = 62.0 kN hangs at point E of the single cantilever truss shown in Fig. 12–81. Use a torque equation for the truss as a whole to determine the tension F_T in the support cable, and then determine the force $\overrightarrow{F_A}$ on the truss at pin A. Neglect the weight of the trusses, which is small compared to the load.

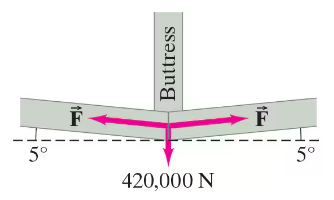
The subterranean tension ring that surrounds the dome in Fig. 12–39 exerts the balancing horizontal force on the abutments for the dome and is 36-sided, so each segment makes a 10° angle with the adjacent one (Fig. 12–83). Calculate the tension F that must exist in each segment so that the required force of 4.2 x 10⁵ N can be exerted at each corner (Example 12–14).

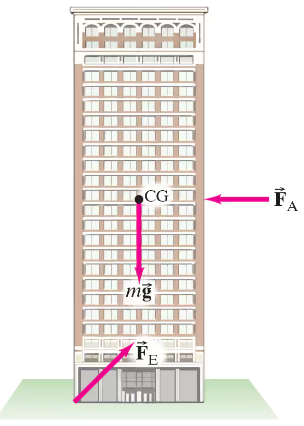
A 50-story building is being planned. It is to be 180.0 m high with a base 46.0 m by 76.0 m. Its total mass will be about 1.8 x 10⁷ kg, and its weight therefore about 1.8 x 10⁸ N. Suppose a 200-km/h wind exerts a force of 950N/m² over the 76.0-m-wide face (Fig. 12–86). Calculate the torque about the potential pivot point, the rear edge of the building (where $\overrightarrow{F_E}$ acts in Fig. 12–86), and determine whether the building will topple. Assume the total force of the wind acts at the midpoint of the building’s face, and that the building is not anchored in bedrock. [Hint: $\overrightarrow{F_E}$ in Fig. 12–86 represents the force that the Earth would exert on the building in the case where the building would just begin to tip.]

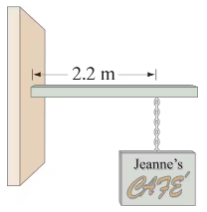
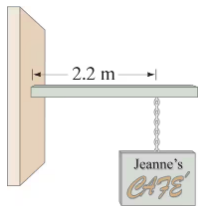
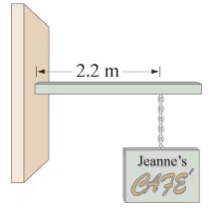
A pole projects horizontally from the front wall of a shop. A 6.1-kg sign hangs from the pole at a point 2.2 m from the wall (Fig. 12–88). What is the torque due to this sign calculated about the point where the pole meets the wall?

A pole projects horizontally from the front wall of a shop. A 6.1-kg sign hangs from the pole at a point 2.2 m from the wall (Fig. 12–88). If the pole is not to fall off, there must be another torque exerted to balance it. What exerts this torque? Use a diagram to show how this torque must act.

A pole projects horizontally from the front wall of a shop. A 6.1-kg sign hangs from the pole at a point 2.2 m from the wall (Fig. 12–88). Discuss whether compression, tension, and/or shear play a role in part (b).

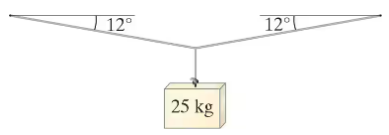
When a mass of 25 kg is hung from the middle of a fixed straight aluminum wire, the wire sags to make an angle of 12° with the horizontal as shown in Fig. 12–90. Determine the radius of the wire.

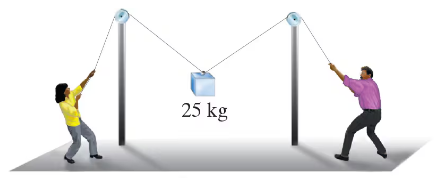
A 25-kg object is being lifted by two people pulling on the ends of a 1.15-mm-diameter nylon cord that goes over two 3.00-m-high poles that are 4.5 m apart, as shown in Fig. 12–93. How high above the floor will the object be when the cord breaks?

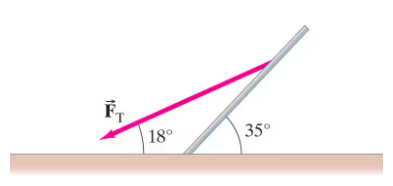
A uniform 95-kg flagpole of length 8.4 m is being erected by pulling on a rope attached 2/3 of the way to the top (Fig. 12–94). When the pole is inclined at 35° and the rope makes an angle with the ground of 18°, what is the tension in the rope?

A steel rod of radius R = 15 cm and length ℓ₀ stands upright on a firm surface. A 78-kg man climbs atop the rod. When a metal is compressed, each atom throughout its bulk moves closer to its neighboring atom by exactly the same fractional amount. If iron atoms in steel are normally 2.0 x 10⁻¹⁰ m apart, by what distance did this interatomic spacing have to change in order to produce the normal force required to support the man? [Note: Neighboring atoms repel each other, and this repulsion accounts for the observed normal force.]

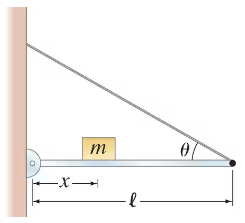
A uniform beam of mass M and length ℓ is mounted on a hinge at a wall as shown in Fig. 12–101. It is held in a horizontal position by a wire making an angle θ as shown. A mass m is placed on the beam a distance x from the wall, and this distance can be varied. Determine, as a function of x, the components of the force exerted by the beam on the hinge.

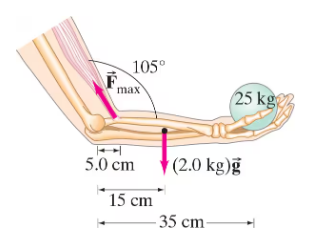
If 25 kg is the maximum mass m that a person can hold in a hand when the arm is positioned with a 105° angle at the elbow as shown in Fig. 12–102, what is the maximum force Fₘₐₓ that the biceps muscle exerts on the forearm? Assume the forearm and hand have a total mass of 2.0 kg with a cg that is 15 cm from the elbow, and that the biceps muscle attaches 5.0 cm from the elbow.

Suppose a 65-kg person jumps from a height of 3.0 m down to the ground. Estimate the stress and determine if the tibia will break in a stiff-legged landing (d = 1.0 cm).