Back
BackProblem 1
By how much does the gravitational potential energy of a 58-kg pole vaulter change if her center of mass rises 4.0 m during the jump?
Problem 2
You drop a basketball from a height of 5.0 m, which rebounds to a new height of 3.0 m. How much energy is lost to nonconservative forces? Give your answer as percentage of the initial energy.
Problem 4a
A 66.5-kg hiker starts at an elevation of 1150 m and climbs to the top of a peak 2660 m high. What is the hiker’s change in potential energy?
Problem 7
A particle is constrained to move in one dimension along the x axis and is acted upon by a force given by = - (k/x³) î, where k is a constant with units appropriate to the SI system. Find the potential energy function U(x), if U is arbitrarily defined to be zero at x = 2.0m, so that U (2.0m) = 0.
Problem 11
A novice skier, starting from rest, slides down an icy frictionless 8.0° incline whose vertical height is 115 m. How fast is she going when she reaches the bottom?
Problem 17
A 1400-kg car moving on a horizontal surface has speed v = 85 km/h when it strikes a horizontal coiled spring and is brought to rest in a distance of 2.2 m. What is the spring constant of the spring? Ignore any thermal energy produced in the collision.
Problem 19a
A vertical spring (ignore its mass), whose spring constant is 875 N/m, is attached to a table and is compressed down by 0.220 m. What upward speed can it give to a 0.380-kg ball when released?
Problem 22c
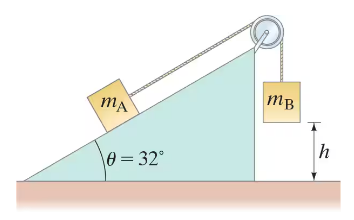
Two masses are connected by a string as shown in Fig. 8–35. Mass mA = 3.5 kg rests on a frictionless inclined plane, while mB = 5.0 kg is initially held at a height of h = 0.75 m above the floor. Use conservation of energy to find the velocity of the masses just before mB hits the floor. You should get the same answer as in part (b).
Problem 23a
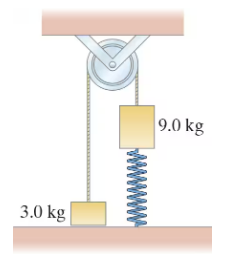
The 9.0-kg mass in Fig. 8–36 is held just barely in contact with a spring for which k = 450 N/m . When that mass is released, it falls, compressing the spring and pulling the 3.0-kg mass up. How far does the 9.0-kg mass fall before momentarily coming to rest? Ignore friction in the pulley.
Problem 24
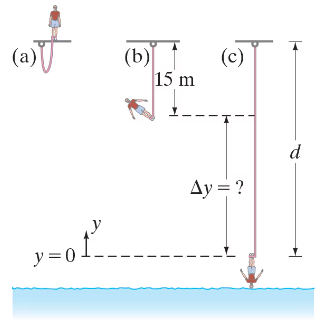
Chris jumps off a bridge with a 15-m-long bungee cord (a heavy stretchable cord) tied around his ankle, Fig. 8–37. He falls 15 m before the bungee cord begins to stretch. Chris’s mass is 75 kg and we assume the cord obeys Hooke’s law, F = -kx with k = 55 N/m. If we neglect air resistance, estimate what distance d below the bridge Chris’s foot will be before coming to a stop. Ignore the mass of the cord (not realistic, however) and treat Chris as a particle.
Problem 26b
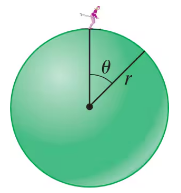
A skier of mass m starts from rest at the top of a solid sphere of radius r and slides down its frictionless surface. If friction is present, does the skier fly off at a greater or lesser angle?
Problem 35
You slide down an 8.0-m-high icy hill (≈ frictionless). At the bottom is a level stretch where the coefficient of kinetic friction is 0.30. How far would you travel across the level stretch?
Problem 36a
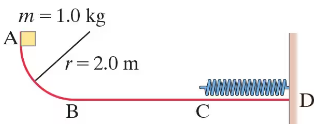
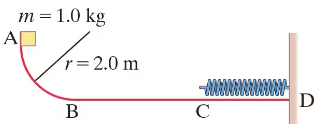
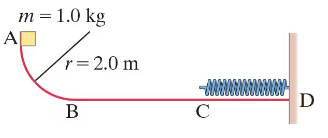
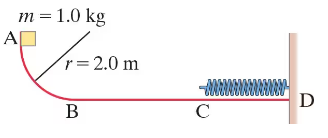
Consider the track shown in Fig. 8–39. The section AB is one quadrant of a circle of radius 2.0 m and is frictionless. B to C is a horizontal span 3.0 m long with a coefficient of kinetic friction μₖ = 0.25. The section CD under the spring is frictionless. A block of mass 1.0 kg is released from rest at A. After sliding on the track, it compresses the spring by 0.20 m. Determine the velocity of the block at point B.
Problem 36b
Consider the track shown in Fig. 8–39. The section AB is one quadrant of a circle of radius 2.0 m and is frictionless. B to C is a horizontal span 3.0 m long with a coefficient of kinetic friction μₖ = 0.25. The section CD under the spring is frictionless. A block of mass 1.0 kg is released from rest at A. After sliding on the track, it compresses the spring by 0.20 m. Determine the thermal energy produced as the block slides from B to C.
Problem 36c
Consider the track shown in Fig. 8–39. The section AB is one quadrant of a circle of radius 2.0 m and is frictionless. B to C is a horizontal span 3.0 m long with a coefficient of kinetic friction μₖ = 0.25. The section CD under the spring is frictionless. A block of mass 1.0 kg is released from rest at A. After sliding on the track, it compresses the spring by 0.20 m. Determine the velocity of the block at point C.
Problem 36d
Consider the track shown in Fig. 8–39. The section AB is one quadrant of a circle of radius 2.0 m and is frictionless. B to C is a horizontal span 3.0 m long with a coefficient of kinetic friction μₖ = 0.25. The section CD under the spring is frictionless. A block of mass 1.0 kg is released from rest at A. After sliding on the track, it compresses the spring by 0.20 m. Determine the stiffness constant k for the spring.
Problem 38b
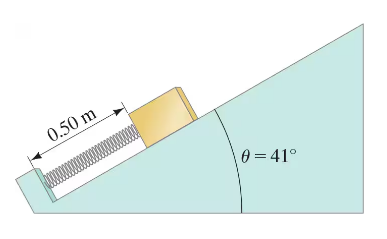
A spring ( k = 75 N/m) has an equilibrium length of 1.00 m. The spring is compressed to a length of 0.50 m and a mass of 2.0 kg is placed at its free end on a frictionless slope which makes an angle of 41° with respect to the horizontal (Fig. 8–41). The spring is then released. If the mass is attached to the spring, how far up the slope will the mass move before coming to rest?
Problem 38c
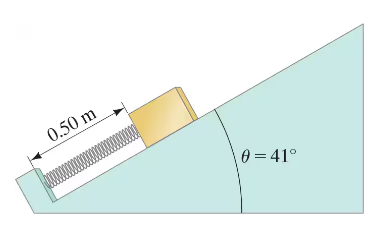
A spring ( k = 75 N/m) has an equilibrium length of 1.00 m. The spring is compressed to a length of 0.50 m and a mass of 2.0 kg is placed at its free end on a frictionless slope which makes an angle of 41° with respect to the horizontal (Fig. 8–41). The spring is then released. Now the incline has a coefficient of kinetic friction μₖ. If the block, attached to the spring, is observed to stop just as it reaches the spring’s equilibrium position, what is the coefficient of friction μₖ?
Problem 40a
Early test flights for the space shuttle used a “glider” (mass of 980 kg including pilot). After a horizontal launch at 480 km/h at a height of 3200 m, the glider eventually landed at sea level with a speed of 210 km/h. What would its landing speed have been in the absence of air resistance?
Problem 44a
Determine the escape velocity from the Sun for an object at the Sun’s surface ( r = 7.0 x 10⁵ km , M = 2.0 x 10³⁰ kg).
Problem 44b
Determine the escape velocity from the Sun for an object at the average distance of the Earth (1.50 x 10⁸ km). Compare (give factor for each) to the speed of the Earth in its orbit.
Problem 57b
An 85-kg football player traveling 5.0 m/s is stopped in 1.0 s by a tackler. What average power is required to stop him?
Problem 62
A driver notices that her 950-kg car, when in neutral, slows down from 95 km/h to 65 km/h in about 7.0 s on a flat horizontal road. Approximately what power (watts and hp) is needed to keep the car traveling at a constant 80 km/h?
Problem 69c
The position of a 280-g object is given (in meters) by x = 4.0t³ - 8.0t² - 44t, where t is in seconds. What is the average net power input during the interval from t = 0s to t = 2.0 s, and in the interval from t = 2.0 s to 4.0 s?
Problem 73a
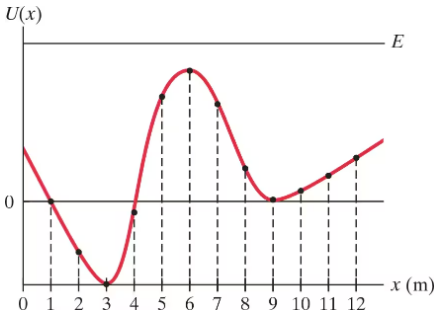
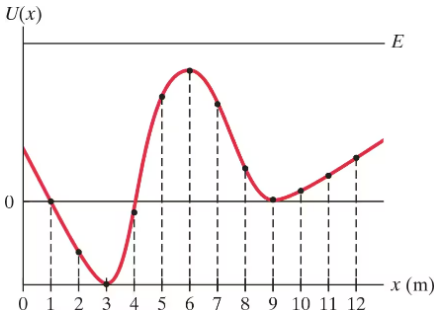
The graph of Fig. 8–43 shows the potential energy curve of a particle moving along the 𝓍 axis under the influence of a conservative force. Note that the total energy E > U(𝓍), so that the particle’s speed is never zero. In which interval(s) of 𝓍 is the force on the particle to the right?
Problem 73b
The graph of Fig. 8–43 shows the potential energy curve of a particle moving along the 𝓍 axis under the influence of a conservative force. Note that the total energy E > U(𝓍), so that the particle’s speed is never zero. At what value(s) of 𝓍 is the magnitude of the force a minimum?
Problem 74a
The potential energy of the two atoms in a diatomic (two-atom) molecule can be approximated as (Lennard-Jones potential) U(r) = -(a/r⁶) + (b/r¹²), where r is the distance between the two atoms and a and b are positive constants. At what values of r is U(r) a minimum? A maximum?
Problem 79b
Water flows slowly over a dam at the rate of 320 kg/s and falls vertically 88 m before striking the turbine blades. Calculate the rate at which mechanical energy is transferred to the turbine blades, assuming 55% efficiency.
Problem 85
If you stand on a bathroom scale, the spring inside the scale compresses 0.60 mm, and it tells you your weight is 760 N. Now if you jump on the scale from a height of 1.0 m, what does the scale read at its peak? Assume Hooke’s law holds.
Problem 95
Proper design of automobile braking systems must account for heat buildup under heavy braking. Calculate the thermal energy dissipated from brakes in a 1500-kg car that descends a 17° hill. The car begins braking when its speed is 95 km/h and slows to a speed of 35 km/h in a distance of 0.30 km measured along the road.