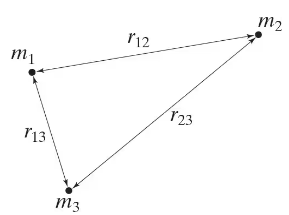
Suppose we have three masses, m₁ , m₂ and m₃, that initially are extremely (≈ infinitely) far apart from each other. The work needed to bring them to the positions shown in Fig. 8–50 is W = - G ((m₁m₂/ r₁₂) + (m₁m₃/r₁₃) + (m₂m₃/r₂₃)). Is W equal to the binding energy of the system—that is, is W equal to the energy required to separate the components by an infinite distance? Explain.

How much work can a 3.0-hp motor do in 1.0h?

The two atoms in a diatomic molecule exert an attractive force on each other at large distances and a repulsive force at short distances. The magnitude of the force between two atoms in a diatomic molecule can be approximated by the Lennard-Jones force, or F(r) = F₀ [2(σ/r)¹³ - (σ/r)⁷], where r is the separation between the two atoms, and σ and F₀ are constants. For an oxygen molecule (which is diatomic) F₀ = 9.60 x 10⁻¹¹ N and σ = 3.50 x 100⁻¹¹ m. Integrate the equation for F(r) to determine the potential energy U(r) of the oxygen molecule.