An isotonic solution contains 0.90% NaCl mass to volume. Calculate the percent mass to volume for isotonic solutions containing each solute at 25 °C. Assume a van't Hoff factor of 1.9 for all ionic solutes. a. KCl

When HNO2 is dissolved in water, it partially dissociates according to the equation HNO2 ⇌ H+ + NO2-. A solution is prepared that contains 7.050 g of HNO2 in 1.000 kg of water. Its freezing point is -0.2929 °C. Calculate the fraction of HNO2 that has dissociated.
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
Dissociation of Acids

Freezing Point Depression

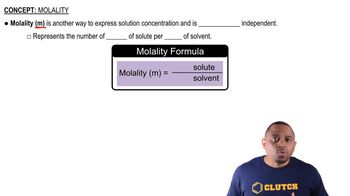
Molality
Magnesium citrate, Mg3(C6H5O7)2, belongs to a class of laxatives called hyperosmotics, which cause rapid emptying of the bowel. When a concentrated solution of magnesium citrate is consumed, it passes through the intestines, drawing water and promoting diarrhea, usually within 6 hours. Calculate the osmotic pressure of a magnesium citrate laxative solution containing 28.5 g of magnesium citrate in 235 mL of solution at 37 °C (approximate body temperature). Assume complete dissociation of the ionic compound.
A solution of a nonvolatile solute in water has a boiling point of 375.3 K. Calculate the vapor pressure of water above this solution at 338 K. The vapor pressure of pure water at this temperature is 0.2467 atm.
The density of a 0.438 M solution of potassium chromate (K2CrO4) at 298 K is 1.063 g/mL. Calculate the vapor pressure of water above the solution. The vapor pressure of pure water at this temperature is 0.0313 atm. (Assume complete dissociation of the solute.)
The vapor pressure of carbon tetrachloride, CCl4, is 0.354 atm, and the vapor pressure of chloroform, CHCl3, is 0.526 atm at 316 K. A solution is prepared from equal masses of these two compounds at this temperature. Calculate the mole fraction of the chloroform in the vapor above the solution. If the vapor above the original solution is condensed and isolated into a separate flask, what will the vapor pressure of chloroform be above this new solution?
