Hydrogen iodide decomposes slowly to H2 and I2 at 600 K. The reaction is second order in HI, and the rate constant is 9.7 * 10^-6 M^-1 s^-1. Assume the initial concentration of HI is 0.100 M. (a) What is its molarity after a reaction time of 6.00 days?

Verified step by step guidance

Identify the rate law for a second-order reaction: \( \text{Rate} = k[\text{HI}]^2 \), where \( k \) is the rate constant.

Use the integrated rate law for a second-order reaction: \( \frac{1}{[\text{HI}]} = \frac{1}{[\text{HI}]_0} + kt \), where \([\text{HI}]_0\) is the initial concentration, \([\text{HI}]\) is the concentration at time \( t \), and \( k \) is the rate constant.

Convert the reaction time from days to seconds: \( 6.00 \text{ days} \times 24 \text{ hours/day} \times 3600 \text{ seconds/hour} \).

Substitute the known values into the integrated rate law: \( \frac{1}{[\text{HI}]} = \frac{1}{0.100 \text{ M}} + (9.7 \times 10^{-6} \text{ M}^{-1} \text{ s}^{-1}) \times \text{time in seconds} \).

Solve for \([\text{HI}]\) to find the molarity after 6.00 days.

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Second-Order Reactions

A second-order reaction is one where the rate of reaction is proportional to the square of the concentration of one reactant or to the product of the concentrations of two reactants. For a reaction of the form A → products, the rate law can be expressed as rate = k[A]^2. This means that as the concentration of A decreases, the rate of reaction also decreases, which is crucial for calculating concentration changes over time.

Integrated Rate Law

The integrated rate law for a second-order reaction provides a relationship between concentration and time. It is given by the equation 1/[A] = 1/[A0] + kt, where [A] is the concentration at time t, [A0] is the initial concentration, k is the rate constant, and t is the time elapsed. This equation allows us to calculate the concentration of a reactant after a specific time period.

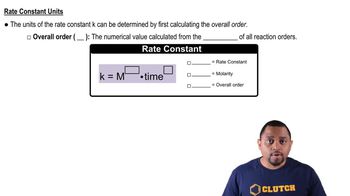
Units of Rate Constant

The units of the rate constant (k) are essential for ensuring dimensional consistency in rate equations. For a second-order reaction, the units of k are M^-1 s^-1, indicating that the rate of reaction depends on the concentration squared. Understanding these units helps in correctly applying the integrated rate law and interpreting the results of concentration calculations over time.

Recommended video:

Guided course

00:45

Rate Constant Units

Related Practice

Textbook Question

Initial rate data at 25 °C are listed in the table for the reaction NH4 +1aq2 + NO2 -1aq2S N21g2 + 2 H2O1l2 (b) What is the value of the rate constant?

Textbook Question

Trimethylamine and chlorine dioxide react in water in an electron transfer reaction to form the trimethylamine cation and chlorite ion: 1CH323 N1aq2 + ClO21aq2 + H2O1l2S 1CH323 NH+1aq2 + ClO2 -1aq2 + OH-1aq2 Initial rate data obtained at 23 °C are listed in the following table. (b) What would be the initial rate in an experiment with initial concentrations 31CH323 N4 = 4.2 * 10-2 M and 3ClO24 = 3.4 * 10-2 M?

Textbook Question

What is the half-life (in minutes) of the reaction in Problem 14.74 when the initial C4H6 concentration is 0.0200 M? How many minutes does it take for the concentration of C4H6 to drop from 0.0100 M to 0.0050 M?

Textbook Question

The decomposition of N2O5 is a first-order reaction. At 25 °C, it takes 5.2 h for the concentration to drop from 0.120 M to 0.060 M. How many hours does it take for the concentration to drop from 0.030 M to 0.015 M? From 0.480 M to 0.015 M?

Textbook Question

You wish to determine the reaction order and rate constant for the following thermal decomposition reaction: AB2 S 1>2 A2 + B2 (c) Describe how you would determine the value of the rate constant.