The decomposition of N2O5 is a first-order reaction. At 25 °C, it takes 5.2 h for the concentration to drop from 0.120 M to 0.060 M. How many hours does it take for the concentration to drop from 0.030 M to 0.015 M? From 0.480 M to 0.015 M?

Verified step by step guidance

Identify that the decomposition of \( \text{N}_2\text{O}_5 \) is a first-order reaction, which means the rate of reaction depends on the concentration of \( \text{N}_2\text{O}_5 \) raised to the first power.

Use the first-order rate equation: \( \ln \left( \frac{[A]_0}{[A]} \right) = kt \), where \([A]_0\) is the initial concentration, \([A]\) is the concentration at time \(t\), and \(k\) is the rate constant.

Calculate the rate constant \(k\) using the given data: \([A]_0 = 0.120 \text{ M}\), \([A] = 0.060 \text{ M}\), and \(t = 5.2 \text{ h}\). Rearrange the equation to solve for \(k\): \(k = \frac{1}{t} \ln \left( \frac{[A]_0}{[A]} \right)\).

Once \(k\) is determined, use it to find the time \(t\) for the concentration to drop from \(0.030 \text{ M}\) to \(0.015 \text{ M}\) using the same first-order rate equation.

Similarly, use the calculated \(k\) to find the time \(t\) for the concentration to drop from \(0.480 \text{ M}\) to \(0.015 \text{ M}\) using the first-order rate equation.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.

Video duration:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

First-Order Reactions

First-order reactions are chemical reactions where the rate is directly proportional to the concentration of one reactant. This means that as the concentration decreases, the rate of reaction also decreases. The integrated rate law for a first-order reaction can be expressed as ln([A]0/[A]) = kt, where [A]0 is the initial concentration, [A] is the concentration at time t, k is the rate constant, and t is time.

Half-Life of a Reaction

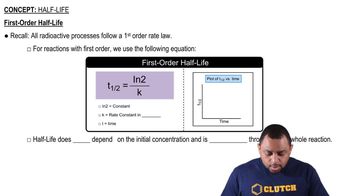
The half-life of a reaction is the time required for the concentration of a reactant to decrease to half of its initial value. For first-order reactions, the half-life is constant and does not depend on the initial concentration. This property allows for straightforward calculations of time intervals for concentration changes, as the time taken for each successive half-life remains the same.

Rate Constant (k)

The rate constant (k) is a proportionality factor in the rate equation that relates the rate of a reaction to the concentration of reactants. For first-order reactions, k can be determined from the slope of a plot of ln([A]) versus time. Knowing the rate constant allows for the calculation of reaction times for different concentration changes, as it remains constant at a given temperature.