Some watch dials are coated with a phosphor, like ZnS, and a polymer in which some of the 1H atoms have been replaced by 3H atoms, tritium. The phosphor emits light when struck by the beta particle from the tritium decay, causing the dials to glow in the dark. The half-life of tritium is 12.3 yr. If the light given off is assumed to be directly proportional to the amount of tritium, by how much will a dial be dimmed in a watch that is 50 yr old?
Ch.21 - Nuclear Chemistry

Brown15th EditionChemistry: The Central ScienceISBN: 9780137542970Not the one you use?Change textbook
Chapter 21, Problem 38
How much time is required for a 6.25-mg sample of 51Cr to decay to 0.75 mg if it has a half-life of 27.8 days?
 Verified step by step guidance
Verified step by step guidance1
Step 1: Understand the concept of half-life, which is the time required for half of a radioactive substance to decay. In this problem, the half-life of 51Cr is given as 27.8 days.
Step 2: Use the formula for exponential decay: \( N = N_0 \times (\frac{1}{2})^{\frac{t}{t_{1/2}}} \), where \( N \) is the remaining quantity, \( N_0 \) is the initial quantity, \( t \) is the time elapsed, and \( t_{1/2} \) is the half-life.
Step 3: Substitute the given values into the formula: \( 0.75 = 6.25 \times (\frac{1}{2})^{\frac{t}{27.8}} \).
Step 4: Solve for \( t \) by first dividing both sides by 6.25 to isolate the exponential term: \( (\frac{1}{2})^{\frac{t}{27.8}} = \frac{0.75}{6.25} \).
Step 5: Take the natural logarithm of both sides to solve for \( t \): \( \ln((\frac{1}{2})^{\frac{t}{27.8}}) = \ln(\frac{0.75}{6.25}) \), and use the property of logarithms to bring down the exponent: \( \frac{t}{27.8} \cdot \ln(\frac{1}{2}) = \ln(\frac{0.75}{6.25}) \). Solve for \( t \).
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Half-life
Half-life is the time required for half of a sample of a radioactive substance to decay. It is a constant property of each radioactive isotope, indicating how quickly it transforms into a more stable form. In this question, the half-life of 51Cr is given as 27.8 days, which will be crucial for calculating the time needed for the sample to decay from 6.25 mg to 0.75 mg.
Recommended video:
Guided course

Zero-Order Half-life
Exponential Decay
Exponential decay describes the process by which a quantity decreases at a rate proportional to its current value. In radioactive decay, the amount of substance remaining decreases exponentially over time, which can be modeled mathematically. This concept is essential for understanding how the mass of 51Cr will reduce over successive half-lives until it reaches the desired amount.
Recommended video:
Guided course
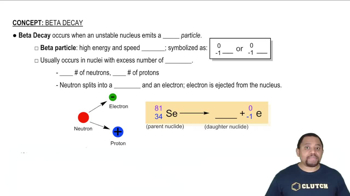
Beta Decay
Decay Formula
The decay formula, often expressed as N(t) = N0 * (1/2)^(t/T), relates the remaining quantity of a substance (N(t)) to its initial quantity (N0), the time elapsed (t), and the half-life (T). This formula allows us to calculate the time required for a sample to decay to a specific amount, making it a key tool for solving the given problem regarding the decay of 51Cr.
Recommended video:
Guided course

Beta Decay
Related Practice
Textbook Question
1
views
Textbook Question
It takes 4 h 39 min for a 2.00-mg sample of radium-230 to decay to 0.25 mg. What is the half-life of radium-230?
Textbook Question
Cobalt-60 is a strong gamma emitter that has a half-life of 5.26 yr. The cobalt-60 in a radiotherapy unit must be replaced when its radioactivity falls to 75% of the original sample. If an original sample was purchased in June 2021, when will it be necessary to replace the cobalt-60?
Textbook Question
The cloth shroud from around a mummy is found to have a 14C activity of 9.7 disintegrations per minute per gram of carbon as compared with living organisms that undergo 16.3 disintegrations per minute per gram of carbon. From the half-life for 14C decay, 5730 yr, calculate the age of the shroud.
