It takes 4 h 39 min for a 2.00-mg sample of radium-230 to decay to 0.25 mg. What is the half-life of radium-230?

Verified step by step guidance

Identify the initial mass \( m_0 = 2.00 \text{ mg} \) and the final mass \( m = 0.25 \text{ mg} \).

Note the time taken for this decay is 4 hours and 39 minutes, which needs to be converted to minutes: \( 4 \times 60 + 39 = 279 \text{ minutes} \).

Use the first-order decay formula: \( m = m_0 \times \left( \frac{1}{2} \right)^{\frac{t}{t_{1/2}}} \), where \( t \) is the time elapsed and \( t_{1/2} \) is the half-life.

Rearrange the formula to solve for the half-life \( t_{1/2} \): \( t_{1/2} = \frac{t}{\log_2\left(\frac{m_0}{m}\right)} \).

Substitute the known values into the equation to find \( t_{1/2} \).

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.

Video duration:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Radioactive Decay

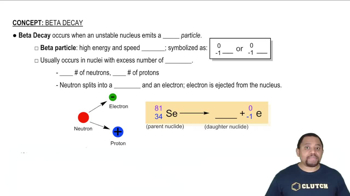
Radioactive decay is the process by which an unstable atomic nucleus loses energy by emitting radiation. This process occurs at a predictable rate for each radioactive isotope, characterized by its half-life, which is the time required for half of the radioactive atoms in a sample to decay.

Half-Life

Half-life is a specific measure of the time it takes for half of a given quantity of a radioactive substance to decay. It is a constant for each isotope and is crucial for calculating the remaining quantity of the substance over time, as well as for understanding the decay process in nuclear chemistry.

Exponential Decay Formula

The exponential decay formula describes how the quantity of a radioactive substance decreases over time. It is expressed as N(t) = N0 * (1/2)^(t/T), where N(t) is the remaining quantity at time t, N0 is the initial quantity, and T is the half-life. This formula allows for the calculation of remaining mass after a certain period, which is essential for solving decay problems.

Recommended video:

Guided course

03:01

Beta Decay

Related Practice

Textbook Question

Some watch dials are coated with a phosphor, like ZnS, and a polymer in which some of the 1H atoms have been replaced by 3H atoms, tritium. The phosphor emits light when struck by the beta particle from the tritium decay, causing the dials to glow in the dark. The half-life of tritium is 12.3 yr. If the light given off is assumed to be directly proportional to the amount of tritium, by how much will a dial be dimmed in a watch that is 50 yr old?

views

Textbook Question

Cobalt-60 is a strong gamma emitter that has a half-life of 5.26 yr. The cobalt-60 in a radiotherapy unit must be replaced when its radioactivity falls to 75% of the original sample. If an original sample was purchased in June 2021, when will it be necessary to replace the cobalt-60?