Cobalt-60 is a strong gamma emitter that has a half-life of 5.26 yr. The cobalt-60 in a radiotherapy unit must be replaced when its radioactivity falls to 75% of the original sample. If an original sample was purchased in June 2021, when will it be necessary to replace the cobalt-60?

Verified step by step guidance

Identify the half-life of cobalt-60, which is given as 5.26 years.

Use the formula for exponential decay: \( N = N_0 \times (0.5)^{t/T_{1/2}} \), where \( N \) is the remaining quantity, \( N_0 \) is the initial quantity, \( t \) is the time elapsed, and \( T_{1/2} \) is the half-life.

Set \( N/N_0 = 0.75 \) because the activity falls to 75% of the original.

Rearrange the formula to solve for \( t \): \( 0.75 = (0.5)^{t/5.26} \).

Solve for \( t \) using logarithms: \( t = 5.26 \times \frac{\log(0.75)}{\log(0.5)} \).

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.

Video duration:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Half-life

Half-life is the time required for half of the radioactive nuclei in a sample to decay. For Cobalt-60, which has a half-life of 5.26 years, this means that after this period, only 50% of the original amount remains. Understanding half-life is crucial for calculating how long it takes for a radioactive substance to reach a certain level of activity.

Radioactive decay

Radioactive decay is the process by which an unstable atomic nucleus loses energy by emitting radiation. This decay occurs at a predictable rate, characterized by the half-life, and leads to a decrease in the amount of the radioactive isotope over time. In the context of Cobalt-60, it is important to know how much of the substance remains after a certain period to determine when it needs to be replaced.

Exponential decay

Exponential decay describes the process where the quantity of a substance decreases at a rate proportional to its current value. In radioactive decay, this means that the amount of Cobalt-60 decreases exponentially over time, allowing us to calculate the remaining quantity after a specific number of half-lives. This concept is essential for determining when the radioactivity of the cobalt-60 falls to 75% of its original amount.

Recommended video:

Guided course

03:01

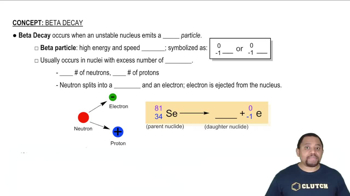
Beta Decay

Related Practice

Textbook Question

Some watch dials are coated with a phosphor, like ZnS, and a polymer in which some of the 1H atoms have been replaced by 3H atoms, tritium. The phosphor emits light when struck by the beta particle from the tritium decay, causing the dials to glow in the dark. The half-life of tritium is 12.3 yr. If the light given off is assumed to be directly proportional to the amount of tritium, by how much will a dial be dimmed in a watch that is 50 yr old?

views

Textbook Question

It takes 4 h 39 min for a 2.00-mg sample of radium-230 to decay to 0.25 mg. What is the half-life of radium-230?

Textbook Question

The cloth shroud from around a mummy is found to have a 14C activity of 9.7 disintegrations per minute per gram of carbon as compared with living organisms that undergo 16.3 disintegrations per minute per gram of carbon. From the half-life for 14C decay, 5730 yr, calculate the age of the shroud.