This reaction was monitored as a function of time: A → B + C A plot of ln[A] versus time yields a straight line with slope -0.0045/s. d. If the initial concentration of A is 0.250 M, what is the concentration after 225 s?

Verified step by step guidance

Identify the type of reaction: The problem states that a plot of \( \ln[A] \) versus time yields a straight line, indicating that the reaction is first-order with respect to A.

Use the first-order integrated rate law: \( \ln[A] = -kt + \ln[A]_0 \), where \( k \) is the rate constant, \( t \) is time, \( [A]_0 \) is the initial concentration, and \( [A] \) is the concentration at time \( t \).

Substitute the given values into the equation: \( k = 0.0045 \text{ s}^{-1} \), \( t = 225 \text{ s} \), and \( [A]_0 = 0.250 \text{ M} \).

Rearrange the equation to solve for \( [A] \): \( \ln[A] = -0.0045 \times 225 + \ln(0.250) \).

Calculate \( \ln[A] \) and then exponentiate to find \( [A] \): \( [A] = e^{\ln[A]} \).

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.

Video duration:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

First-Order Reactions

First-order reactions are chemical reactions where the rate is directly proportional to the concentration of one reactant. In this case, the reaction A → B + C is first-order with respect to A, meaning that as the concentration of A decreases, the rate of the reaction also decreases. The relationship can be described by the equation ln[A] = ln[A]₀ - kt, where k is the rate constant.

Natural Logarithm and Linear Relationships

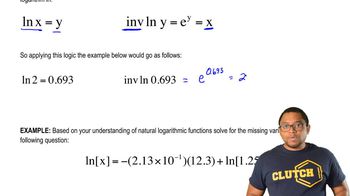
The natural logarithm (ln) is a mathematical function that is often used in kinetics to linearize the relationship between concentration and time for first-order reactions. When plotting ln[A] against time, a straight line indicates a first-order reaction, where the slope of the line is equal to -k. This linear relationship allows for easy determination of the rate constant and concentration changes over time.

Concentration Calculations

To find the concentration of a reactant at a given time, we can use the integrated rate law for first-order reactions. By rearranging the equation ln[A] = ln[A]₀ - kt, we can solve for [A] at any time t. Given the initial concentration and the rate constant, we can calculate the concentration of A after a specified time, which is essential for understanding the progress of the reaction.

Recommended video:

Guided course

07:35

Calculate Concentration of the Basic Form

Related Practice

Textbook Question

This reaction was monitored as a function of time: A → B + C A plot of ln[A] versus time yields a straight line with slope -0.0045/s. a. What is the value of the rate constant (k) for this reaction at this temperature?

Textbook Question

This reaction was monitored as a function of time: A → B + C A plot of ln[A] versus time yields a straight line with slope -0.0045/s. b. Write the rate law for the reaction.

Textbook Question

This reaction was monitored as a function of time: A → B + C A plot of ln[A] versus time yields a straight line with slope -0.0045/s. c. What is the half-life?

Textbook Question

This reaction was monitored as a function of time: AB → A + B A plot of 1/[AB] versus time yields a straight line with a slope of +0.55/Ms.

a. What is the value of the rate constant (k) for this reaction at this temperature?

Textbook Question

This reaction was monitored as a function of time: AB → A + B A plot of 1/[AB] versus time yields a straight line with a slope of +0.55/Ms. b. Write the rate law for the reaction.

Textbook Question

This reaction was monitored as a function of time: AB → A + B A plot of 1/[AB] versus time yields a straight line with a slope of +0.55/Ms. c. What is the half-life when the initial concentration is 0.55 M?