This reaction was monitored as a function of time: A → B + C A plot of ln[A] versus time yields a straight line with slope -0.0045/s. d. If the initial concentration of A is 0.250 M, what is the concentration after 225 s?
Ch.14 - Chemical Kinetics

Chapter 14, Problem 54c
This reaction was monitored as a function of time: AB → A + B A plot of 1/[AB] versus time yields a straight line with a slope of +0.55/Ms. c. What is the half-life when the initial concentration is 0.55 M?
 Verified step by step guidance
Verified step by step guidance1
Identify the order of the reaction. Since a plot of 1/[AB] versus time yields a straight line, the reaction is second order.
Use the second-order half-life formula: \( t_{1/2} = \frac{1}{k[A]_0} \), where \( k \) is the rate constant and \( [A]_0 \) is the initial concentration.
Recognize that the slope of the line in a second-order reaction plot is equal to the rate constant \( k \). Therefore, \( k = 0.55 \text{ M}^{-1}\text{s}^{-1} \).
Substitute the given initial concentration \( [A]_0 = 0.55 \text{ M} \) and the rate constant \( k = 0.55 \text{ M}^{-1}\text{s}^{-1} \) into the half-life formula.
Calculate the half-life using the formula: \( t_{1/2} = \frac{1}{0.55 \times 0.55} \).

Verified video answer for a similar problem:
This video solution was recommended by our tutors as helpful for the problem above.
Video duration:
1mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Rate Laws and Reaction Order
Rate laws describe the relationship between the concentration of reactants and the rate of a chemical reaction. The order of a reaction indicates how the rate is affected by the concentration of each reactant. In this case, the reaction AB → A + B is second-order, as indicated by the linear plot of 1/[AB] versus time, which is characteristic of second-order kinetics.
Recommended video:
Guided course

Rate Law Fundamentals
Half-Life of a Reaction
The half-life of a reaction is the time required for the concentration of a reactant to decrease to half of its initial value. For second-order reactions, the half-life is dependent on the initial concentration of the reactant. The formula for the half-life (t1/2) of a second-order reaction is t1/2 = 1/(k[AB]0), where k is the rate constant and [AB]0 is the initial concentration.
Recommended video:
Guided course
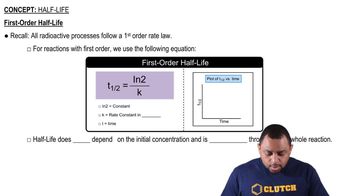
First-Order Half-Life
Slope of the Rate Plot
In the context of reaction kinetics, the slope of the plot of 1/[AB] versus time is equal to the rate constant (k) for a second-order reaction. Given that the slope is +0.55/Ms, this value directly represents the rate constant used in calculating the half-life. Understanding how to interpret the slope is crucial for determining the kinetics of the reaction.
Recommended video:
Guided course
Instantaneous Rate
Related Practice
Textbook Question
Textbook Question
This reaction was monitored as a function of time: AB → A + B A plot of 1/[AB] versus time yields a straight line with a slope of +0.55/Ms.
a. What is the value of the rate constant (k) for this reaction at this temperature?
Textbook Question
This reaction was monitored as a function of time: AB → A + B A plot of 1/[AB] versus time yields a straight line with a slope of +0.55/Ms. b. Write the rate law for the reaction.
Textbook Question
This reaction was monitored as a function of time: AB → A + B A plot of 1/[AB] versus time yields a straight line with a slope of +0.55/Ms.
d. If the initial concentration of AB is 0.250 M, and the reaction mixture initially contains no products, what are the concentrations of A and B after 75 s?
