Back
BackProblem 59
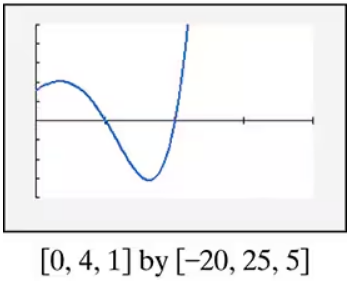
Exercises 53–60 show incomplete graphs of given polynomial functions. a) Find all the zeros of each function. b) Without using a graphing utility, draw a complete graph of the function. f(x)=3x5+2x4−15x3−10x2+12x+8
Problem 59
In Exercises 57–64, find the vertical asymptotes, if any, the horizontal asymptote, if one exists, and the slant asymptote, if there is one, of the graph of each rational function. Then graph the rational function. h(x) = (x^2 - 3x - 4)/(x^2 - x -6)
Problem 60
In Exercises 57–64, find the vertical asymptotes, if any, the horizontal asymptote, if one exists, and the slant asymptote, if there is one, of the graph of each rational function. Then graph the rational function. r(x) = (x^2 + 4x + 3)/(x + 2)^2
Problem 60
Find the inverse of f(x) = x3 + 2
Problem 60
Solve each rational inequality in Exercises 43–60 and graph the solution set on a real number line. Express each solution set in interval notation. x/(x + 2) ≥ 2
Problem 61
Find the domain of each function.
Problem 61
Among all pairs of numbers whose sum is 16, find a pair whose product is as large as possible. What is the maximum product?
Problem 61
Follow the seven steps to graph each rational function. f(x)=2x2/(x2−1)
Problem 62
Find the domain of each function.
Problem 63
Follow the seven steps to graph each rational function. f(x)=−x/(x+1)
Problem 63
Find the domain of each function.
Problem 64
Find the domain of each function.
Problem 64
In Exercises 57–64, find the vertical asymptotes, if any, the horizontal asymptote, if one exists, and the slant asymptote, if there is one, of the graph of each rational function. Then graph the rational function. g(x) = (4x^2 - 16x + 16)/(2x - 3)
Problem 64
Among all pairs of numbers whose difference is 24, find a pair whose product is as small as possible. What is the minimum product?
Problem 65
Follow the seven steps to graph each rational function. f(x)=− 1/(x2−4)
Problem 65
Solve each inequality in Exercises 65–70 and graph the solution set on a real number line. |x2 + 2x - 36| > 12
Problem 67
Solve each inequality in Exercises 65–70 and graph the solution set on a real number line. 3/(x +3) > 3/(x - 2)
Problem 67
Follow the seven steps to graph each rational function. f(x)=2/(x2+x−2)
Problem 68
Solve each inequality in Exercises 65–70 and graph the solution set on a real number line. 1/(x + 1) > 2/(x - 1)
Problem 69
Solve each inequality in Exercises 65–70 and graph the solution set on a real number line.
Problem 69
In Exercises 69–74, solve each inequality and graph the solution set on a real number line. 2x^2 + 5x - 3 < 0
Problem 69
Follow the seven steps to graph each rational function. f(x)=2x2/(x2+4)
Problem 70
In Exercises 69–74, solve each inequality and graph the solution set on a real number line. 2x^2 + 9x + 4 ≥ 0
Problem 71
In Exercises 57–80, follow the seven steps to graph each rational function. f(x)=(x+2)/(x2+x−6)
Problem 71
In Exercises 71–72, use the graph of the polynomial function to solve each inequality.
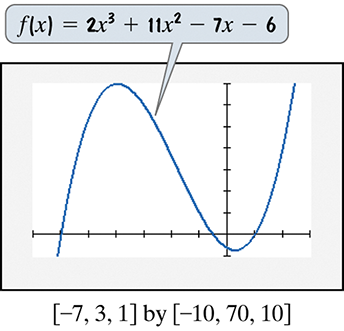
Problem 72
In Exercises 71–72, use the graph of the polynomial function to solve each inequality.
2x3 + 11x2 < 7x + 6

Problem 73
In Exercises 57–80, follow the seven steps to graph each rational function. f(x)=(x−2)/(x2−4)
Problem 73
In Exercises 73–74, use the graph of the rational function to solve each inequality.
1/4(x + 2) ≤ - 3/4(x - 2)

Problem 74
In Exercises 73–74, use the graph of the rational function to solve each inequality.
1/4(x + 2) > - 3/4(x - 2)
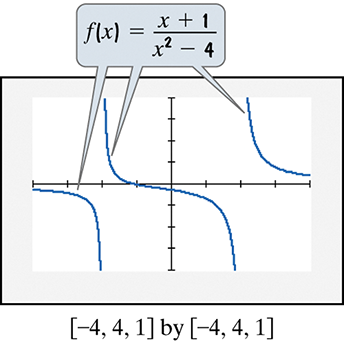
Problem 74
In Exercises 69–74, solve each inequality and graph the solution set on a real number line. (x + 3)/(x - 4) ≤ 5