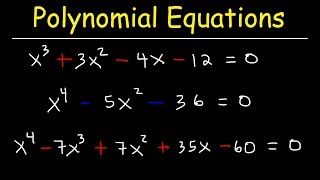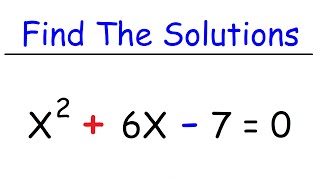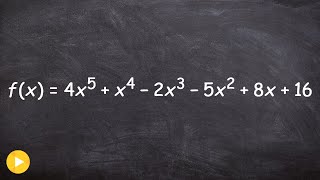4. Polynomial Functions
Zeros of Polynomial Functions
4. Polynomial Functions
Zeros of Polynomial Functions
Use Rational Zero Theorem to Find Possible Rational Zeros
Additional 1 creators.
Learn with other creators
Practice this topic
- Open QuestionIn Exercises 1–8, use the Rational Zero Theorem to list all possible rational zeros for each given function. f(x)=x^3+x^2−4x−4
- Open QuestionDetermine whether each statement is true or false. If false, explain why. The product of a complex number and its conjugate is always a real number.
- Open QuestionIn Exercises 9–16, a) List all possible rational zeros. b) Use synthetic division to test the possible rational zeros and find an actual zero. c) Use the quotient from part (b) to find the remaining zeros of the polynomial function. f(x)=x^3+x^2−4x−4
- Open QuestionIn Exercises 9–16, a) List all possible rational zeros. b) Use synthetic division to test the possible rational zeros and find an actual zero. c) Use the quotient from part (b) to find the remaining zeros of the polynomial function. f(x)=x^3−2x^2−11x+12
Find Zeros of a Polynomial Function
Additional 2 creators.
Learn with other creators
Showing 5 of 5 videos
Practice this topic
- Open QuestionDetermine whether each statement is true or false. If false, explain why. The polynomial function ƒ(x)=2x^5+3x^4-8x^3-5x+6 has three variations in sign.
- Open QuestionIn Exercises 1–8, use the Rational Zero Theorem to list all possible rational zeros for each given function. f(x)=x^5−x^4−7x^3+7x^2−12x−12
- Open QuestionIn Exercises 9–16, a) List all possible rational zeros. b) Use synthetic division to test the possible rational zeros and find an actual zero. c) Use the quotient from part (b) to find the remaining zeros of the polynomial function. f(x)=x^3+4x^2−3x−6
- Open QuestionIn Exercises 17–24, a) List all possible rational roots. b) List all possible rational roots. c) Use the quotient from part (b) to find the remaining roots and solve the equation. x^3−2x^2−11x+12=0
Solve Polynomial Equations
Additional 2 creators.
Learn with other creators
Showing 5 of 5 videos
Practice this topic
- Open QuestionDetermine whether each statement is true or false. If false, explain why. A polynomial function having degree 6 and only real coefficients may have no real zeros.
- Open QuestionIn Exercises 1–8, use the Rational Zero Theorem to list all possible rational zeros for each given function. f(x)=3x^4−11x^3−3x^2−6x+8
- Open QuestionUse the factor theorem and synthetic division to determine whether the second polynomial is a factor of the first. See Example 1. 4x^2+2x+54; x-4
- Open QuestionUse the factor theorem and synthetic division to determine whether the second polynomial is a factor of the first. See Example 1. x^3+2x^2+3; x-1
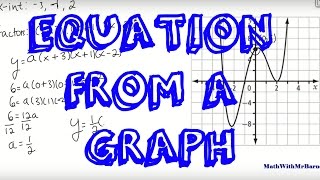
Use the Linear Factorization Theorem to Find Polynomials With Given Zeros
Learn with other creators
Practice this topic
- Open QuestionDetermine whether each statement is true or false. If false, explain why. For ƒ(x)=(x+2)^4(x-3), the number 2 is a zero of multiplicity 4.
- Open QuestionIn Exercises 1–8, use the Rational Zero Theorem to list all possible rational zeros for each given function. f(x)=4x^4−x^3+5x^2−2x−6
- Open QuestionUse the factor theorem and synthetic division to determine whether the second polynomial is a factor of the first. See Example 1. x^3+6x^2-2x-7; x+1
- Open QuestionIf ƒ(x) is a polynomial function with real coefficients, and if 7+2i is a zero of the function, then what other complex number must also be a zero?
Use Descartes's Rule of Signs
Learn with other creators
Practice this topic
- Open QuestionDetermine whether each statement is true or false. If false, explain why. Because x-1 is a factor of ƒ(x)=x^6-x^4+2x^2-2, we can also conclude that ƒ(1)=0
- Open QuestionIn Exercises 1–8, use the Rational Zero Theorem to list all possible rational zeros for each given function. f(x)=3x^4−11x^3−x^2+19x+6
- Open QuestionUse the factor theorem and synthetic division to determine whether the second polynomial is a factor of the first. See Example 1. x^3-5x^2+3x+1; x-1
- Open QuestionIn Exercises 9–16, a) List all possible rational zeros. b) Use synthetic division to test the possible rational zeros and find an actual zero. c) Use the quotient from part (b) to find the remaining zeros of the polynomial function. f(x)=2x^3−3x^2−11x+6