Skip to main content

My Courses

Calculators AI Tools Study Prep Blog Study Prep Home

4. Polynomial Functions

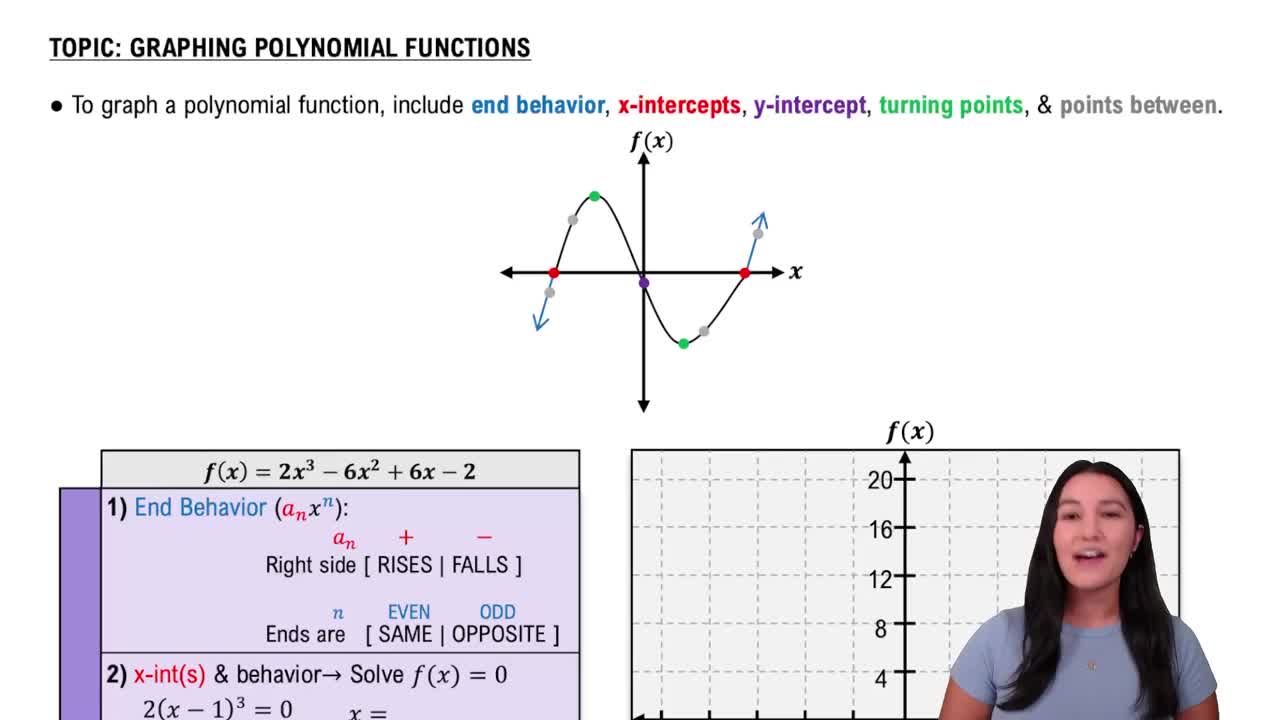
Graphing Polynomial Functions

4. Polynomial Functions

Graphing Polynomial Functions

Guided videos.

Learn with Callie

Go to the course

Identifying Intervals of Unknown Behavior

Identifying Intervals of Unknown Behavior

Graphing Polynomial Functions

Graphing Polynomial Functions

Additional 2 creators.

Learn with other creators

Attributes of Polynomial Functions

Attributes of Polynomial Functions

Even and Odd Symmetries

Even and Odd Symmetries

Practice this topic

Multiple Choice
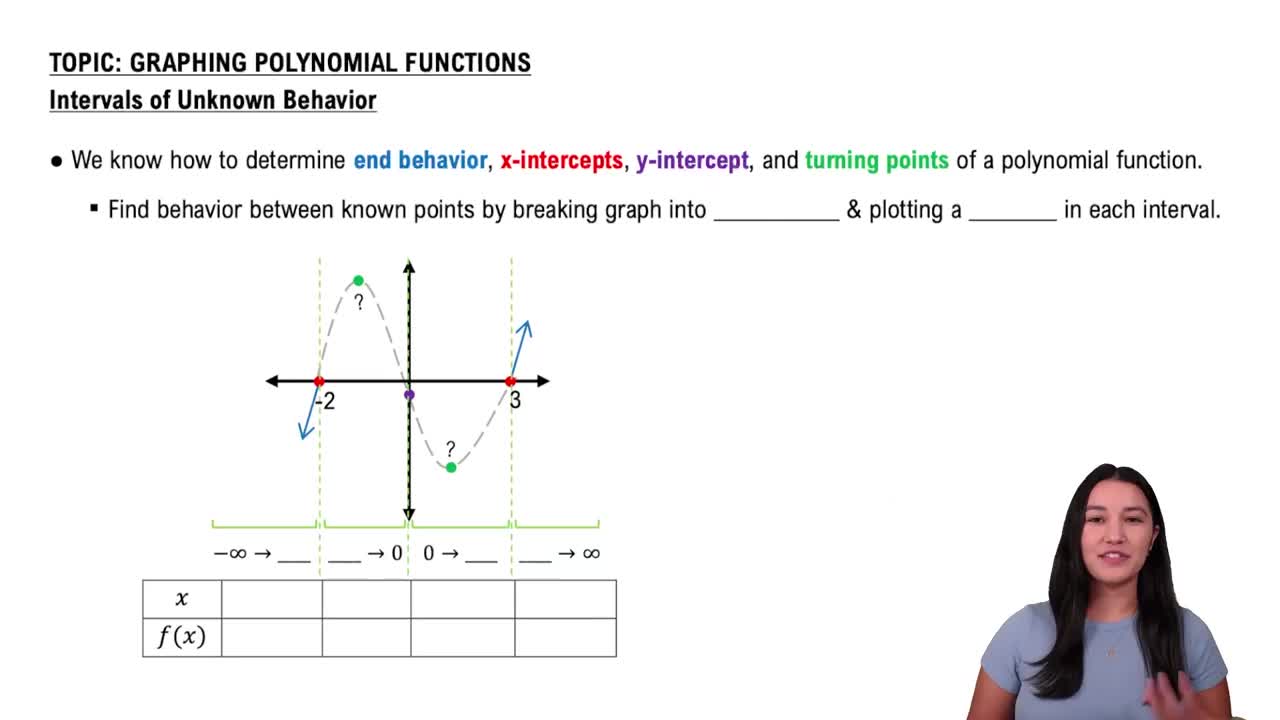
Based on the known points plotted on the graph, determine what intervals the graph should be broken into.
Plotted points are: $\left(-3,0\right),$ $\left(0,1\right),\left(2,0\right),$ & $\left(5,0\right)$
Multiple Choice
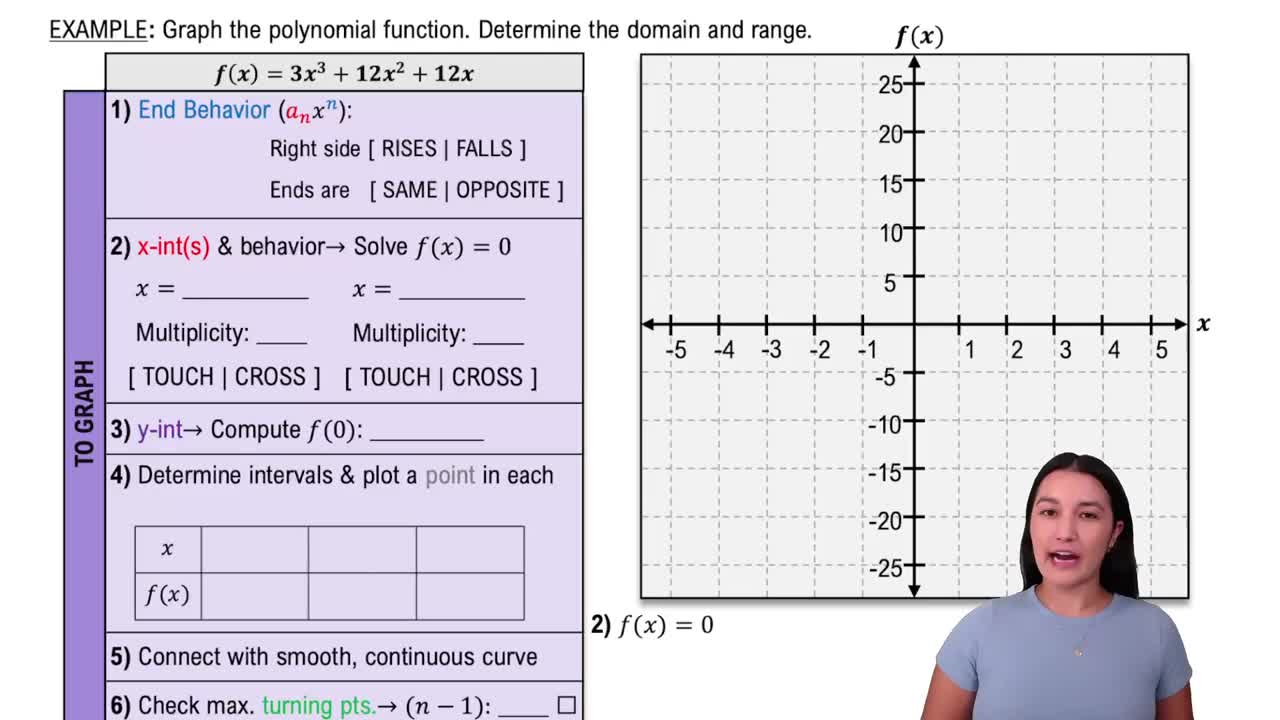
Graph the polynomial function. Determine the domain and range. $f\left(x\right)=\left(3x+2\right)\left(x-1\right)^2$
Open Question
Graph each function. Determine the largest open intervals of the domain over which each function is (a) increasing or (b) decreasing. See Example 1. ƒ(x)=2x^4
Open Question
In Exercises 11–14, identify which graphs are not those of polynomial functions.
Open Question
In Exercises 19–24,(a) Use the Leading Coefficient Test to determine the graph's end behavior.(b) Determine whether the graph has y-axis symmetry, origin symmetry, or neither.(c) Graph the function.f(x) = 4x - x^3
Open Question
In Exercises 33–40, use the Intermediate Value Theorem to show that each polynomial has a real zero between the given integers. f(x)=x^3−4x^2+2; between 0 and 1

Show all questions