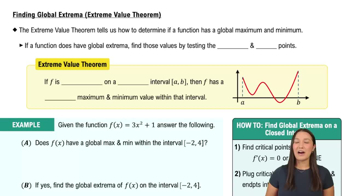
5. Graphical Applications of Derivatives

Find the critical points of the given function.

$g(x)=\frac13x^3-\frac12x^2-12x$

Find the critical points of the given function.

$f(t)=\frac{6t}{t^2+1}$

Find the critical points of the given function.

$f(x)=\sqrt{2-x^2}$

Find the global maximum and minimum values of the function on the given interval. State as ordered pairs.

$y=x+\frac{2}{x};[0.25,3]$

The figure shows six containers, each of which is filled from the top. Assume water is poured into the containers at a constant rate and each container is filled in 10 s. Assume also that the horizontal cross sections of the containers are always circles. Let h (t) be the depth of water in the container at time t, for 0 ≤ t ≤ 10 . <IMAGE>

d. For each container, where does h' (the derivative of h ) have an absolute maximum on [0 , 10]?

Absolute maxima and minima Determine the location and value of the absolute extreme values of ƒ on the given interval, if they exist.

ƒ(x) = x³ - 3x² on [-1, 3]

Absolute maxima and minima Determine the location and value of the absolute extreme values of ƒ on the given interval, if they exist.

ƒ(x) = x² - 10 on [-2, 3]

Increasing and decreasing functions. Find the intervals on which f is increasing and the intervals on which it is decreasing.

f(x) = √2 sin x- x on [0, 2π]