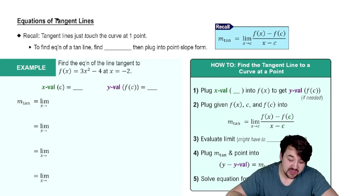
2. Intro to Derivatives

Given the function $f(x)=4x^2-1$, calculate the slope of the tangent line at $x=-3$.

Given the function $f(x)=x^2-10x+2$, calculate the slope of the tangent line at $x=2$.

Given the function $f(x)=x^2+100$, calculate the slope of the tangent line at $x=0$.

Given the function $f(x)=3(x^2-1)$, find the equation of the tangent line at $x=1$.

Average and marginal profit Let C(x) represent the cost of producing x items and p(x) be the sale price per item if x items are sold. The profit P(x) of selling x items is P(x) = xp(c) - C(x) (revenue minus costs). The average profit per item when x items are sold is P(x)/x and the marginal profit is dP/dx. The marginal profit approximates the profit obtained by selling one more item, given that x items have already been sold. Consider the following cost functions C and price functions p.

a. Find the profit function P.

C(x) = −0.02x²+50x+100, p(x)=100−0.1x, a=500

Average and marginal profit Let C(x) represent the cost of producing x items and p(x) be the sale price per item if x items are sold. The profit P(x) of selling x items is P(x) = xp(c) - C(x) (revenue minus costs). The average profit per item when x items are sold is P(x)/x and the marginal profit is dP/dx. The marginal profit approximates the profit obtained by selling one more item, given that x items have already been sold. Consider the following cost functions C and price functions p.

a. Find the profit function P.

C(x) = − 0.04x²+100x+800, p(x)=200, a=1000

Average and marginal profit Let C(x) represent the cost of producing x items and p(x) be the sale price per item if x items are sold. The profit P(x) of selling x items is P(x) = xp(c) - C(x) (revenue minus costs). The average profit per item when x items are sold is P(x)/x and the marginal profit is dP/dx. The marginal profit approximates the profit obtained by selling one more item, given that x items have already been sold. Consider the following cost functions C and price functions p.

a. Find the profit function P.

C(x) = − 0.04x²+100x+800, p(x) = 200−0.1x, a=1000

U.S. population growth The population p(t) (in millions) of the United States t years after the year 1900 is shown in the figure. Approximately when (in what year) was the U.S. population growing most slowly between 1925 and 2020? Estimate the growth rate in that year. <IMAGE>