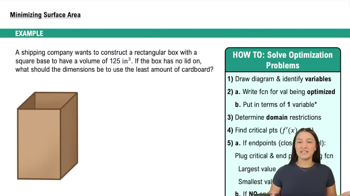
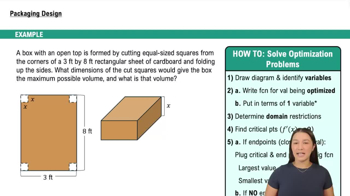
5. Graphical Applications of Derivatives

A poster is set to have a total area of 1150 cm², with 2-cm margins on the sides and the top, and a 3-cm margin at the bottom. What dimensions will maximize the printed area?

Your café sells lattes for $4 each to 100 customers per day. For every $1 increase in price, you would lose 20 customers. Find the price that maximizes revenue. Hint: The # of items sold is based on the number of customers.

Maximizing profit Suppose a tour guide has a bus that holds a maximum of 100 people. Assume his profit (in dollars) for taking people on a city tour is P(n) = n(50 - 0.5n) - 100. (Although P is defined only for positive integers, treat it as a continuous function.)

a. How many people should the guide take on a tour to maximize the profit?

{Use of Tech} Growth rate of spotted owlets The rate of growth (in g/week) of the body mass of Indian spotted owlets is modeled by the function r(t) = 10,147.9e⁻²·²ᵗ/(37.98e⁻²·² + 1), where t is the age (in weeks) of the owlets. What value of t > 0 maximizes r? What is the physical meaning of the maximum value?

{Use of Tech} Demand functions and elasticity Economists use demand functions to describe how much of a commodity can be sold at varying prices. For example, the demand function D(p) = 500 - 10p says that at a price of p = 10, a quantity of D(10) = 400 units of the commodity can be sold. The elasticity E = dD/dp p/D of the demand gives the approximate percent change in the demand for every 1% change in the price. (See Section 3.6 or the Guided Project Elasticity in Economics for more on demand functions and elasticity.)

b. If the price is $12 and increases by 4.5%, what is the approximate percent change in the demand? 

Population models The population of a species is given by the function P(t) = Kt²/(t² + b) , where t ≥ 0 is measured in years and K and b are positive real numbers.

c. For arbitrary positive values of K and b, when does the maximum growth rate occur (in terms of K and b)?