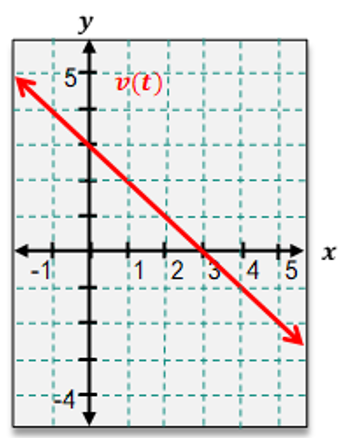
The velocity (/) of a drone flying in the air is given by for hours. Let .
How far has the drone traveled by the time it has reached /?
2.5
4.5
2
6.5
 Verified step by step guidance
Verified step by step guidance
 1:17m
1:17mMaster Using The Velocity Function with a bite sized video explanation from Patrick
Start learning