Hauling in a dinghy A dinghy is pulled toward a dock by a rope from the bow through a ring on the dock 6 ft above the bow. The rope is hauled in at the rate of 2 ft/sec.
a. How fast is the boat approaching the dock when 10 ft of rope are out?
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: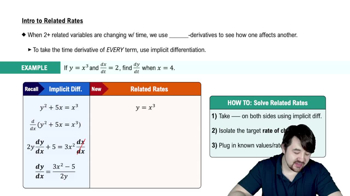

 4:16m
4:16mMaster Intro To Related Rates with a bite sized video explanation from Patrick
Start learning