Area The area A of a triangle with sides of lengths a and b enclosing an angle of measure θ is
A = (1/2) ab sinθ.
b. How is dA/dt related to dθ/dt and da/dt if only b is constant?
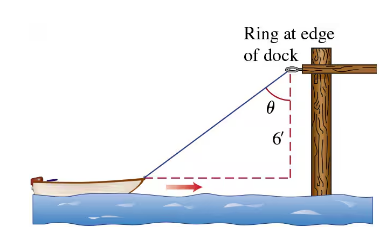
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:


 4:16m
4:16mMaster Intro To Related Rates with a bite sized video explanation from Patrick
Start learning