Heating a plate When a circular plate of metal is heated in an oven, its radius increases at the rate of 0.01 cm/min. At what rate is the plate’s area increasing when the radius is 50 cm?
Table of contents
- 0. Functions7h 54m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 31m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
4. Applications of Derivatives
Related Rates
Problem 3.8.32b
Textbook Question
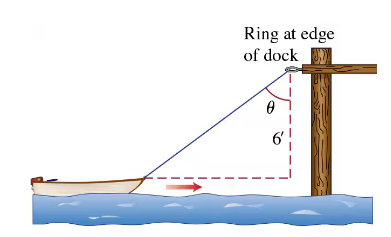
Hauling in a dinghy A dinghy is pulled toward a dock by a rope from the bow through a ring on the dock 6 ft above the bow. The rope is hauled in at the rate of 2 ft/sec.
b. At what rate is the angle θ changing at this instant (see the figure)?
 Verified step by step guidance
Verified step by step guidance1
First, identify the relationship between the variables involved. We have a right triangle where the vertical side is 6 ft (the height of the ring above the bow), the hypotenuse is the length of the rope, and the angle θ is formed between the rope and the horizontal line from the bow to the dock.
Use trigonometric relationships to express the angle θ in terms of the length of the rope. Specifically, use the sine function: sin(θ) = opposite/hypotenuse = 6/L, where L is the length of the rope.
Differentiate the equation sin(θ) = 6/L with respect to time t to find the rate of change of the angle θ. This involves implicit differentiation. Remember that dL/dt is given as -2 ft/sec (since the rope is being pulled in, the length is decreasing).
Apply the chain rule to differentiate: d(sin(θ))/dt = cos(θ) * dθ/dt and d(6/L)/dt = -6/L^2 * dL/dt. Set these two derivatives equal to each other: cos(θ) * dθ/dt = -6/L^2 * (-2).
Solve for dθ/dt, the rate at which the angle θ is changing. Substitute the known values into the equation, including the current length of the rope if needed, to find the expression for dθ/dt.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
7mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Related Rates
Related rates involve finding the rate at which one quantity changes with respect to another. In this problem, the rate at which the rope is hauled in affects the rate at which the angle θ changes. By using derivatives, we can relate these rates and solve for the unknown rate of change of θ.
Recommended video:
Intro To Related Rates
Trigonometric Relationships
Trigonometric relationships are essential for understanding how the angle θ changes as the rope is pulled. The problem involves a right triangle formed by the rope, the vertical distance from the dock to the bow, and the horizontal distance from the dock to the dinghy. Using trigonometric functions like sine or cosine can help express θ in terms of these distances.
Recommended video:

Introduction to Trigonometric Functions
Implicit Differentiation
Implicit differentiation is used when dealing with equations involving multiple variables that are not easily separated. In this scenario, the relationship between the angle θ, the length of the rope, and the distances involved can be differentiated implicitly to find the rate of change of θ with respect to time, given the rate at which the rope is pulled.
Recommended video:

Finding The Implicit Derivative

 4:16m
4:16mWatch next
Master Intro To Related Rates with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
