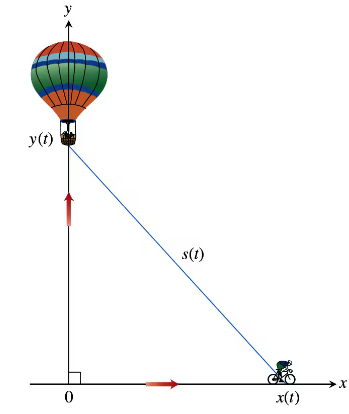
A sliding ladder
A 13-ft ladder is leaning against a house when its base starts to slide away. By the time the base is 12 ft from the house, the base is moving at the rate of 5 ft/sec.
b. At what rate is the area of the triangle formed by the ladder, wall, and ground changing then?