Here are the essential concepts you must grasp in order to answer the question correctly.
Limits
A limit is a fundamental concept in calculus that describes the behavior of a function as its input approaches a certain value. It helps determine the value that a function approaches, which may not necessarily be the function's value at that point. Understanding limits is crucial for analyzing continuity, derivatives, and integrals.
Recommended video:
Graphical Interpretation of Limits
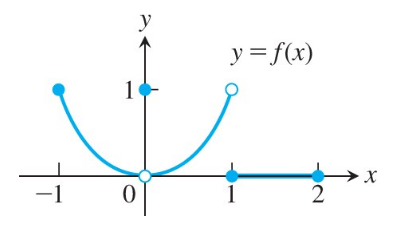
Graphically, the limit of a function as x approaches a certain value can be observed by examining the behavior of the function's graph near that point. If the function approaches a specific y-value from both the left and right sides as x approaches a given point, the limit exists. This visual approach aids in understanding whether a limit is finite, infinite, or does not exist.
Recommended video:
Finding Limits Numerically and Graphically
Existence of Limits
For a limit to exist at a point, the left-hand limit and right-hand limit must both exist and be equal. If there is a discontinuity, such as a jump or an asymptote, the limit may not exist. Evaluating the existence of limits is essential for determining the continuity of a function at a specific point.
Recommended video:
Cases Where Limits Do Not Exist
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:

 6:47m
6:47m