Slope of a Curve at a Point
In Exercises 7–18, use the method in Example 3 to find (a) the slope of the curve at the given point P, and (b) an equation of the tangent line at P.
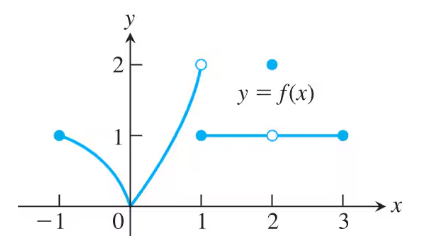
y=x³−3x²+4, P(2,0)
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:

 6:47m
6:47mMaster Finding Limits Numerically and Graphically with a bite sized video explanation from Patrick
Start learning