Here are the essential concepts you must grasp in order to answer the question correctly.
Limits
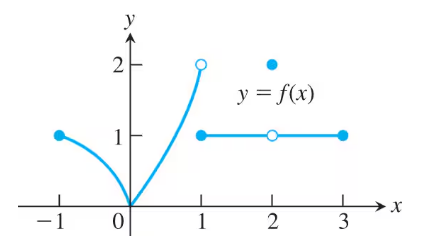
A limit is a fundamental concept in calculus that describes the behavior of a function as its input approaches a certain value. It helps in understanding how functions behave near specific points, even if they are not defined at those points. For example, the limit of f(x) as x approaches 1 from the left (denoted as lim x→1− f(x)) examines the values f(x) takes as x gets closer to 1 from values less than 1.
Recommended video:
One-Sided Limits
One-sided limits refer to the limits of a function as the input approaches a specific value from one side only. The left-hand limit (lim x→c− f(x)) considers values approaching c from the left, while the right-hand limit (lim x→c+ f(x)) considers values approaching c from the right. Understanding one-sided limits is crucial for analyzing functions that may have different behaviors on either side of a point.
Recommended video:
Graphical Interpretation of Limits
Graphical interpretation of limits involves analyzing the graph of a function to determine the value that the function approaches as the input approaches a certain point. By observing the behavior of the graph near that point, one can visually assess whether the limit exists and what its value is. This method is particularly useful for identifying discontinuities or jumps in the function's values.
Recommended video:
Finding Limits Numerically and Graphically
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:


 6:47m
6:47m