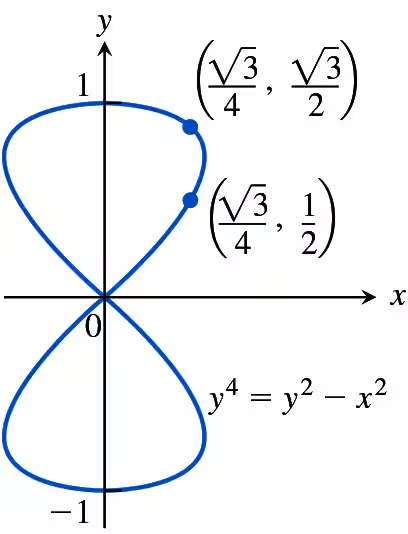
In Exercises 29 and 30, find the slope of the curve at the given points.
y² + x² = y⁴ – 2x at (–2,1) and (–2,–1)
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:



 5:14m
5:14mMaster Finding The Implicit Derivative with a bite sized video explanation from Patrick
Start learning