The eight curve Find the slopes of the curve y⁴ = y² – x² at the two points shown here.
Table of contents
- 0. Functions7h 54m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 31m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
4. Applications of Derivatives
Implicit Differentiation
Problem 3.7.49
Textbook Question
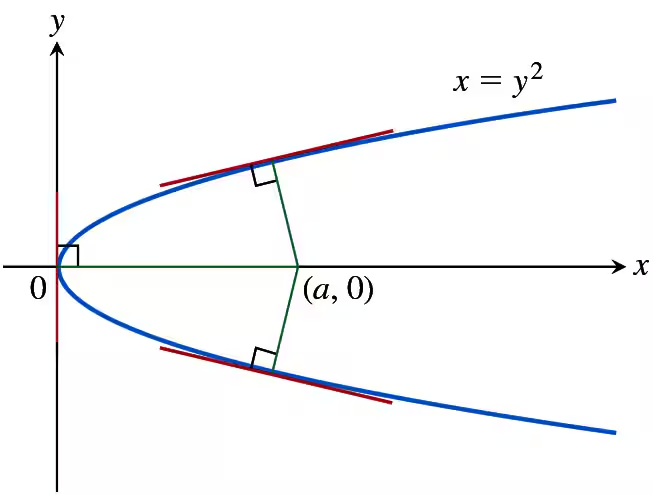
Normal lines to a parabola Show that if it is possible to draw three normal lines from the point (a, 0) to the parabola x = y² shown in the accompanying diagram, then a must be greater than 1/2. One of the normal lines is the x-axis. For what value of a are the other two normal lines perpendicular?
 Verified step by step guidance
Verified step by step guidance1
Step 1: Begin by understanding the geometry of the problem. The parabola is given as x = y², and the point (a, 0) lies on the x-axis. A normal line to the parabola is perpendicular to the tangent line at a given point on the curve. The goal is to show that three normal lines can be drawn from (a, 0) to the parabola only if a > 1/2, and to find the value of a for which the other two normal lines are perpendicular.
Step 2: Find the slope of the tangent line to the parabola at any point (x, y). The derivative of x = y² with respect to y is dx/dy = 2y. The slope of the tangent line is therefore 2y. The slope of the normal line, being perpendicular to the tangent line, is -1/(2y).
Step 3: Write the equation of the normal line passing through a point (x₀, y₀) on the parabola. The equation is given by: x - x₀ = (-1/(2y₀))(y - y₀). Substitute x₀ = y₀² (from the parabola equation) into this normal line equation.
Step 4: To find the intersection of the normal line with the point (a, 0), substitute x = a and y = 0 into the normal line equation derived in Step 3. This will yield a relationship between a and y₀. Solve this equation to determine the values of y₀ for which the normal line passes through (a, 0).
Step 5: Analyze the resulting equation to determine the conditions under which three solutions for y₀ exist. This corresponds to three normal lines passing through (a, 0). Show that this is possible only if a > 1/2. Then, determine the specific value of a for which the other two normal lines are perpendicular by examining the slopes of these lines and ensuring their product equals -1.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
10mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Normal Line to a Curve
A normal line to a curve at a given point is a line perpendicular to the tangent line at that point. For a curve defined by a function, the slope of the normal line is the negative reciprocal of the slope of the tangent line. In the context of the parabola x = y², finding the normal line involves determining the derivative to get the tangent slope and then using it to find the normal slope.
Recommended video:

Slopes of Tangent Lines
Parabola and its Properties
A parabola is a symmetric curve defined by a quadratic equation. In this case, the parabola is given by x = y², which opens to the right. Key properties include its vertex, axis of symmetry, and the fact that it is symmetric about the x-axis. Understanding these properties helps in analyzing how lines, such as normals, interact with the parabola.
Recommended video:
Properties of Parabolas
Perpendicular Lines
Two lines are perpendicular if the product of their slopes is -1. This concept is crucial when determining conditions under which two normal lines to a curve are perpendicular. In the problem, it involves setting up equations based on the slopes of the normal lines and solving for the parameter a to find when the lines are perpendicular.
Recommended video:

Slopes of Tangent Lines

 5:14m
5:14mWatch next
Master Finding The Implicit Derivative with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
