Textbook Question
Slopes, Tangent Lines, and Normal Lines
In Exercises 31–40, verify that the given point is on the curve and find the lines that are (a) tangent and (b) normal to the curve at the given point.
y = 2 sin(πx – y), (1,0)
4. Applications of Derivatives
Implicit Differentiation
4:22 minutesProblem 3.7.45
Textbook Question
The devil’s curve (Gabriel Cramer, 1750) Find the slopes of the devil’s curve y⁴ – 4y² = x⁴ – 9x² at the four indicated points.
Verified step by step guidance1
To find the slopes of the devil's curve at the given points, we need to differentiate the equation of the curve implicitly with respect to x. The equation is y^4 - 4y^2 = x^4 - 9x^2.
Differentiate both sides of the equation with respect to x. For the left side, use the chain rule: d/dx(y^4 - 4y^2) = 4y^3(dy/dx) - 8y(dy/dx). For the right side, differentiate directly: d/dx(x^4 - 9x^2) = 4x^3 - 18x.
Set the derivatives equal to each other: 4y^3(dy/dx) - 8y(dy/dx) = 4x^3 - 18x. Factor out dy/dx from the left side: dy/dx(4y^3 - 8y) = 4x^3 - 18x.
Solve for dy/dx to find the slope: dy/dx = (4x^3 - 18x) / (4y^3 - 8y). This expression gives the slope of the tangent line to the curve at any point (x, y).
Substitute each of the given points into the expression for dy/dx to find the slope at those points. The points are (-3, 2), (-3, -2), (3, 2), and (3, -2).
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Implicit Differentiation
Implicit differentiation is a technique used to find the derivative of a function defined implicitly by an equation involving both x and y. Instead of solving for y explicitly, we differentiate both sides of the equation with respect to x, treating y as a function of x. This method is particularly useful for curves like the devil's curve, where y cannot be easily isolated.
Recommended video:
05:14
Finding The Implicit Derivative
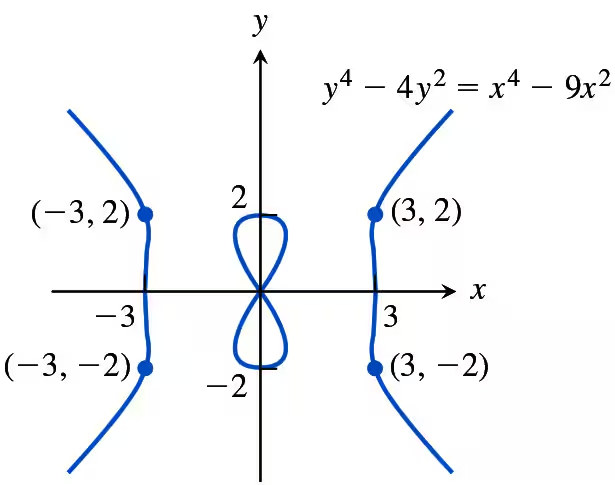
Finding Slopes at Specific Points
To find the slope of a curve at specific points, we evaluate the derivative at those points. The slope of the tangent line to the curve at a given point is represented by the derivative value at that point. For the devil's curve, we will substitute the coordinates of the indicated points into the derivative obtained from implicit differentiation to find the slopes.
Recommended video:
05:45Understanding Slope Fields
Critical Points and Behavior of Curves
Critical points are where the derivative of a function is zero or undefined, indicating potential local maxima, minima, or points of inflection. Understanding the behavior of the curve around these points helps in analyzing the overall shape and direction of the curve. For the devil's curve, identifying critical points can provide insights into the nature of the slopes at the specified coordinates.
Recommended video:
04:50Critical Points
5:14mWatch next
Master Finding The Implicit Derivative with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice