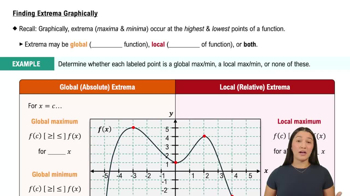
In Exercises 9–66, graph the function using appropriate methods from the graphing procedures presented just before Example 9, identifying the coordinates of any local extreme points and inflection points. Then find coordinates of absolute extreme points, if any.
y = 1 / (x² - 1)