Determine if the function f ( x ) f\left(x\right) f ( x ) is continuous and/or differentiable at x = 2 x=2 x = 2 .

Let's see how we can solve this problem. So here we're asked to determine if the function f of x is continuous and or differentiable at x equals 2. Now, whenever solving these types of problems, our first step should always be to determine whether or not the function is continuous. And notice we have a piecewise function over here. So since we're looking for the continuity in this piecewise function at a certain value, x equals 2, I'm gonna set the left side equal to the right side and replace the x's that I see with 2. So we're going to have the top part that we have right here, this piece, which is going to be 2 cubed, and I'm going to set that equal to this bottom piece, which is going to be 2 minus 2 squared. Notice I'm just replacing x with 2. Now 2 cubed, that's 8. And 2 minus 2 squared, well, that's the same thing as 0 squared, and 0 squared is just 0. Now clearly, 8 does not equal 0. So we can say that this function is not continuous since the two sides did not equal each other at our value of interest. And because we are not continuous, by default, that means we're not going to be differentiable. So this function is neither continuous nor differentiable. Hope you found this video helpful.

2. Intro to Derivatives

Differentiability

Business Calculus

2. Intro to Derivatives

Differentiability

Struggling with Business Calculus?

Join thousands of students who trust us to help them ace their exams!Watch the first video

Multiple Choice

Determine if the function $f\left(x\right)$ is continuous and/or differentiable at $x=2$ .

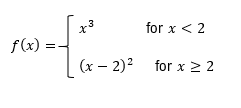
Continuous and non-differentiable

Continuous and differentiable

Discontinuous and non-differentiable

Discontinuous and differentiable

Verified step by step guidance

Step 1: To determine if the function is continuous at x=2, check if the left-hand limit (as x approaches 2 from the left) equals the right-hand limit (as x approaches 2 from the right) and if both equal f(2). For x < 2, f(x) = x^3, and for x ≥ 2, f(x) = (x - 2)^2.

Step 2: Calculate the left-hand limit of f(x) as x approaches 2 from the left. Substitute x=2 into the expression x^3 to find the value of the limit.

Step 3: Calculate the right-hand limit of f(x) as x approaches 2 from the right. Substitute x=2 into the expression (x - 2)^2 to find the value of the limit.

Step 4: Compare the left-hand limit, right-hand limit, and f(2). If all three values are equal, the function is continuous at x=2. If not, the function is discontinuous at x=2.

Step 5: To determine differentiability at x=2, check if the derivative of f(x) from the left-hand side equals the derivative from the right-hand side at x=2. Compute the derivative of x^3 for x < 2 and the derivative of (x - 2)^2 for x ≥ 2, then evaluate both derivatives at x=2 and compare their values.