13: Intro to Differential Equations
Slope Fields
Struggling with Business Calculus?
Join thousands of students who trust us to help them ace their exams!Watch the first videoMultiple Choice
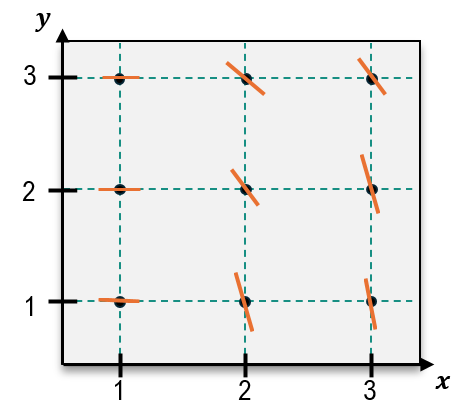
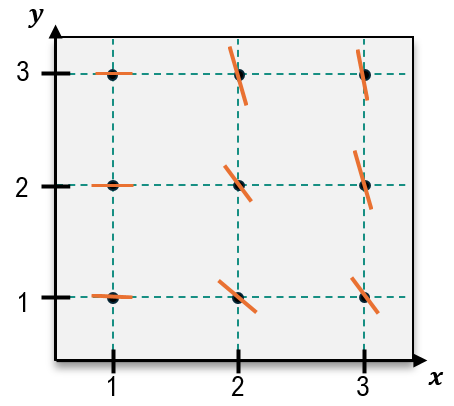
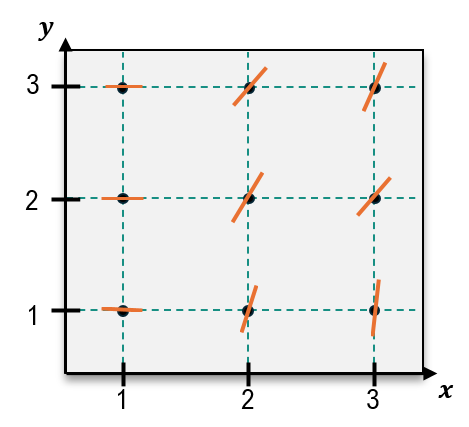
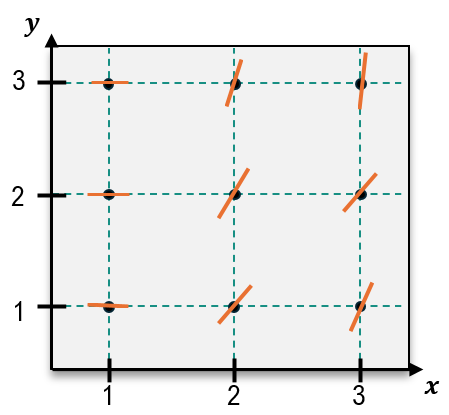
Sketch a slope field for the following differential equation through the nine points shown on the graph.
A
B
C
D
Verified step by step guidance1
Step 1: Understand the differential equation y′ = y - xy. This equation describes the slope of the tangent line at any point (x, y) in the plane.
Step 2: Identify the nine points on the graph where the slope field needs to be sketched. These points are (1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2), and (3,3).
Step 3: For each point, substitute the x and y values into the differential equation y′ = y - xy to calculate the slope at that point. For example, at (1,1), the slope is y′ = 1 - (1)(1) = 0.
Step 4: Draw a small line segment at each point with the calculated slope. For instance, at (1,1), the slope is 0, so the line segment is horizontal. At (2,3), the slope is y′ = 3 - (2)(3) = -3, so the line segment is steeply downward.
Step 5: Repeat this process for all nine points, ensuring the slope field visually represents the behavior of the differential equation across the grid.
5:45mWatch next
Master Understanding Slope Fields with a bite sized video explanation from Patrick
Start learningRelated Videos
0
