Given the right triangle below, evaluate .
Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles40m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
2. Trigonometric Functions on Right Triangles
Trigonometric Functions on Right Triangles
Struggling with Trigonometry?
Join thousands of students who trust us to help them ace their exams!Watch the first videoMultiple Choice
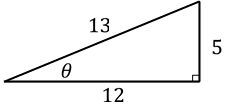
Given the right triangle below, use the sine function to write a trigonometric expression for the missing angle θ.
A
θ=sin−1(135)
B
θ=sin−1(1312)
C
θ=sin−1(125)
D
θ=sin−1(1213)
 Verified step by step guidance
Verified step by step guidance1
Identify the sides of the right triangle: the hypotenuse is 13, the opposite side to angle θ is 5, and the adjacent side is 12.
Recall the definition of the sine function in a right triangle: sin(θ) = opposite/hypotenuse.
Substitute the known values into the sine function: sin(θ) = 5/13.
To find the angle θ, use the inverse sine function: θ = sin⁻¹(5/13).
This expression, θ = sin⁻¹(5/13), represents the measure of the angle θ in terms of the sine function.

 6:4m
6:4mWatch next
Master Introduction to Trigonometric Functions with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Multiple Choice
Trigonometric Functions on Right Triangles practice set


