Polar Coordinate System: Videos & Practice Problems

In mathematics, the polar coordinate system offers a unique way to represent points in a two-dimensional space using the coordinates \( r \) and \( \theta \) instead of the traditional \( x \) and \( y \) used in the Cartesian coordinate system. Here, \( r \) denotes the distance from the pole (the origin) and \( \theta \) represents the angle measured from the polar axis, which corresponds to the positive x-axis in Cartesian coordinates.

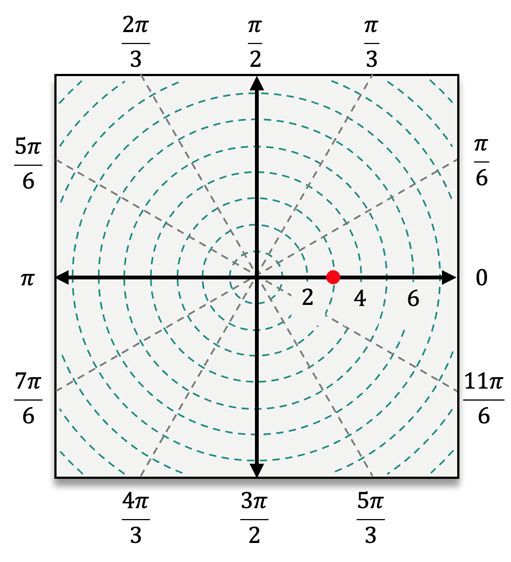
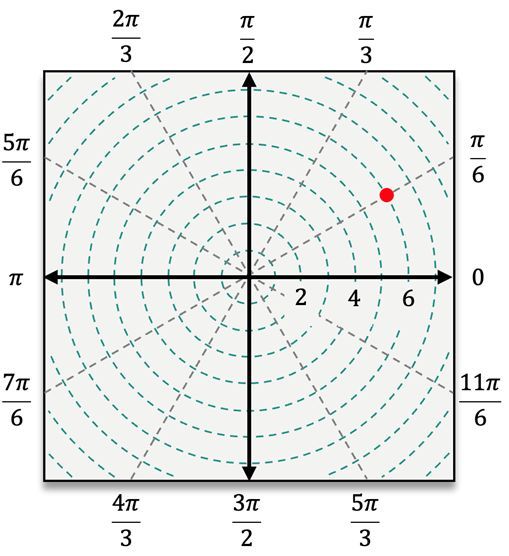
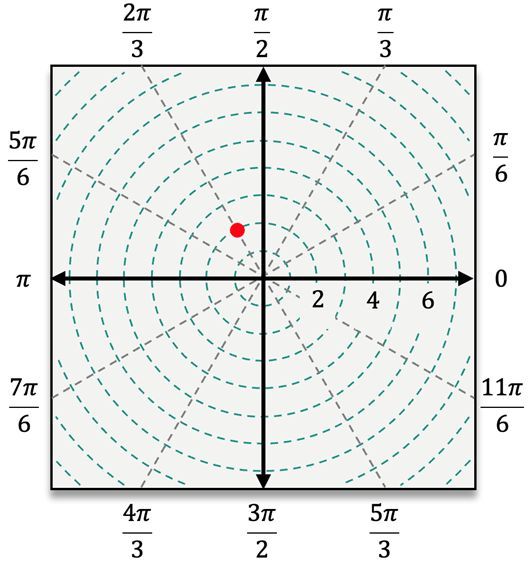
To understand polar coordinates, it is essential to visualize the pole at the origin, where \( r = 0 \). As \( r \) increases, it indicates the distance from the pole, with each value of \( r \) corresponding to a circle centered at the pole. The angle \( \theta \) is measured counterclockwise from the polar axis, similar to how angles are measured on the unit circle. For example, an ordered pair in polar coordinates is expressed as \( (r, \theta) \), such as \( (5, \frac{\pi}{6}) \), where \( r = 5 \) indicates the point is 5 units away from the pole, and \( \theta = \frac{\pi}{6} \) indicates the angle from the polar axis.

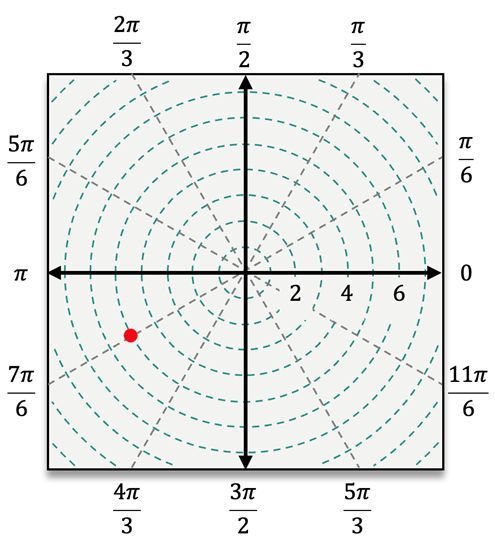
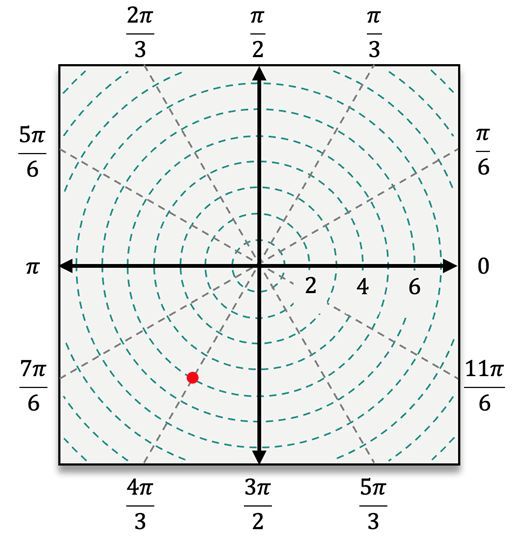
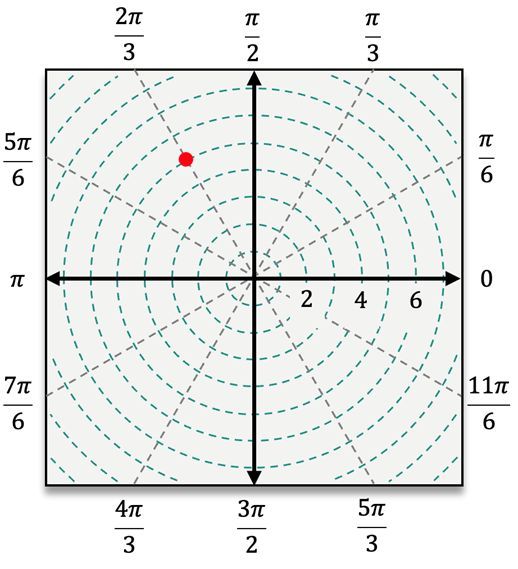
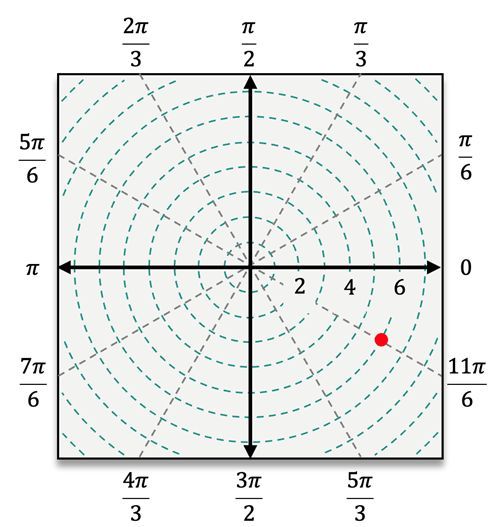
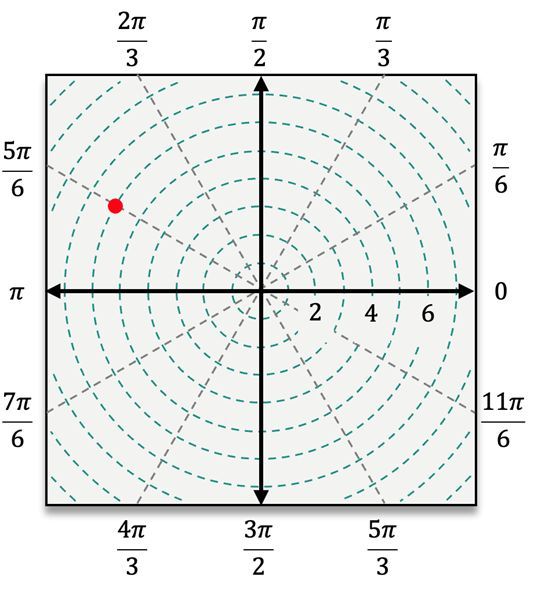
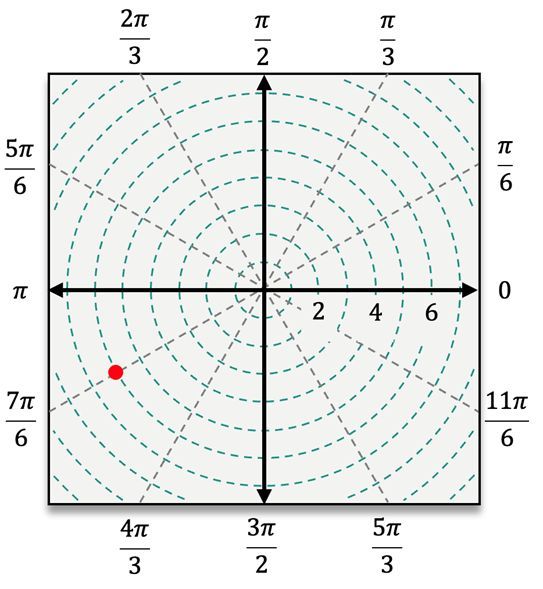
When plotting points in polar coordinates, the process begins by locating the angle \( \theta \) on the polar coordinate system. After identifying the angle, the next step is to count \( r \) units away from the pole. If \( r \) is positive, you move outward in the direction of \( \theta \). However, if \( r \) is negative, you will count in the opposite direction, effectively reflecting the point across the pole.

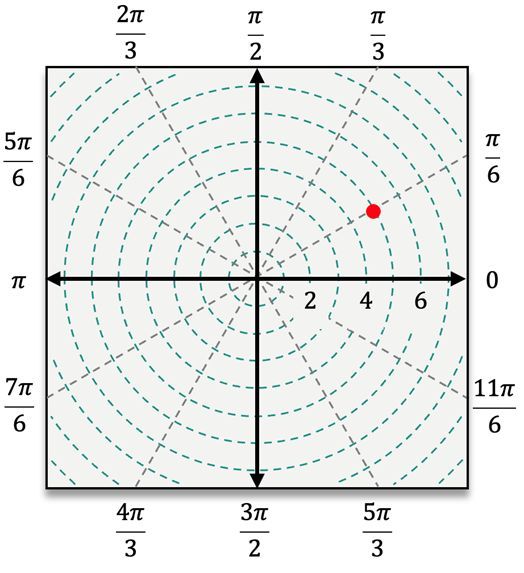
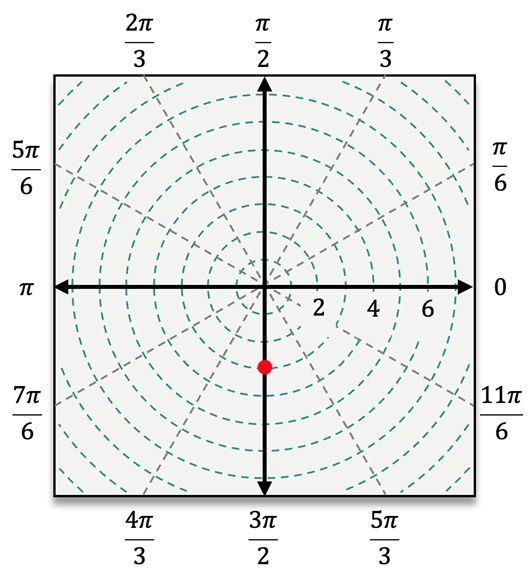
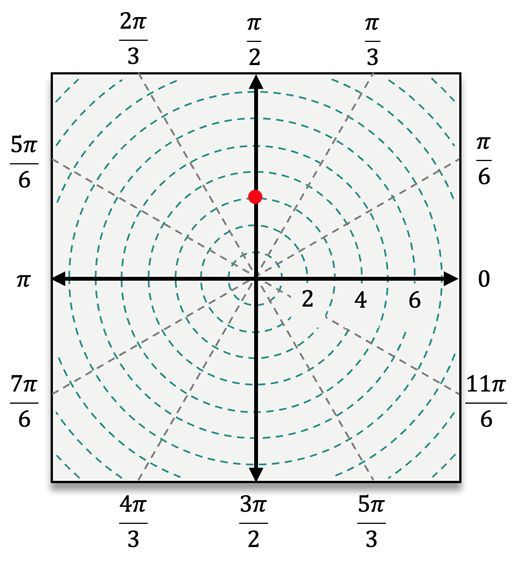
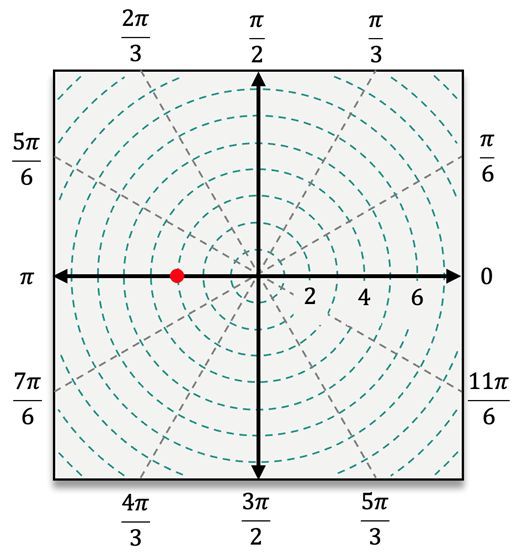
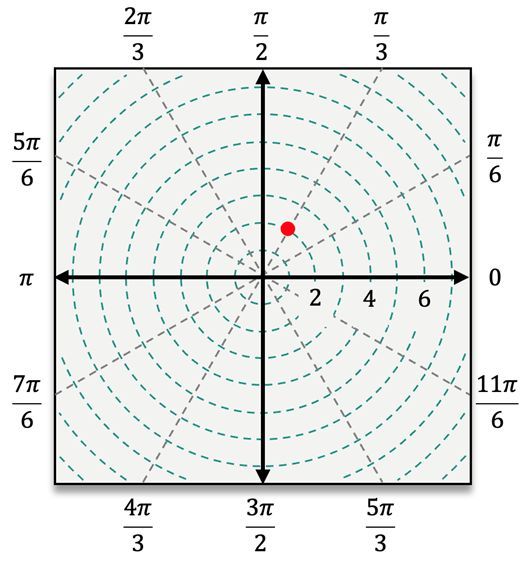
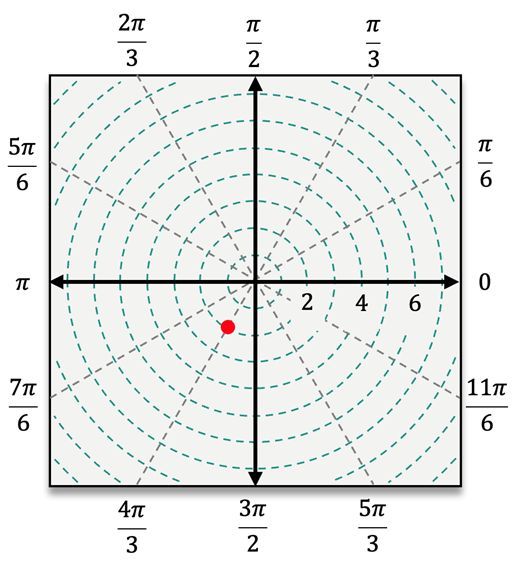
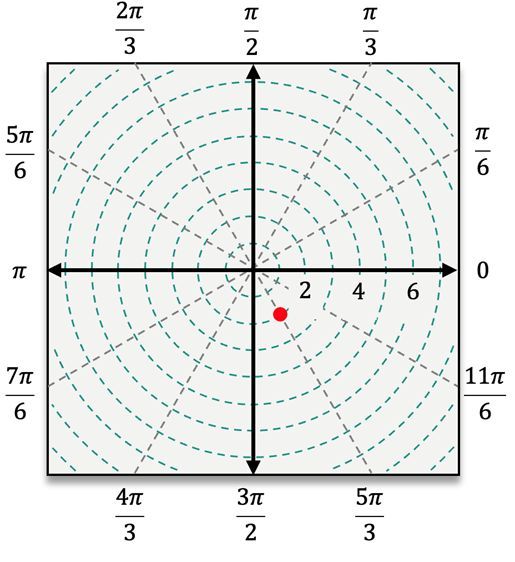
For instance, to plot the point \( (4, \frac{\pi}{3}) \), you first locate the angle \( \frac{\pi}{3} \) and then move 4 units away from the pole. In contrast, for the point \( (5, -\frac{\pi}{3}) \), you would measure the angle \( -\frac{\pi}{3} \) clockwise from the polar axis and then count 5 units outward. When dealing with a negative radius, such as in the point \( (-3, \frac{\pi}{6}) \), you would first locate \( \frac{\pi}{6} \) and then count 3 units in the opposite direction from the pole.

Understanding the signs of both \( r \) and \( \theta \) is crucial when working with polar coordinates, as they dictate the direction and distance from the pole. This system is particularly useful in various fields, including physics and engineering, where circular motion and angular relationships are prevalent.

In polar coordinates, points are defined by a radius (r) and an angle (θ). When plotting these points, it's essential to first identify the angle before determining the position based on the radius. Angles can be expressed in both degrees and radians, which is crucial for accurate plotting.

For example, consider point A, which has coordinates (5, 60°). Here, the radius is 5, and the angle is 60 degrees, equivalent to \(\frac{\pi}{3}\) radians. To plot this point, locate the angle of 60 degrees on the polar coordinate system, then move outward along that line to a distance of 5 units, marking point A.

Next, point B is represented as (3, 90°). The radius is 3, and the angle is 90 degrees, or \(\frac{\pi}{2}\) radians. After locating the 90-degree angle, extend 3 units along that line to find point B.

Point C is given as (0, -\(\frac{5\pi}{3}\)). The radius here is 0, meaning regardless of the angle, the point will be at the origin (the pole). The negative angle indicates a clockwise measurement, but since the radius is 0, point C remains at the origin.

Finally, point D is defined by the coordinates (2, \(\frac{7\pi}{3}\)). The angle \(\frac{7\pi}{3}\) represents a full rotation plus an additional \(\frac{\pi}{3}\) radians. After completing the rotation, you would plot point D by moving 2 units outward along the corresponding line.

In summary, plotting points in polar coordinates involves determining the angle first, followed by measuring the radius from the pole. Understanding the relationship between degrees and radians, as well as how to interpret positive and negative angles, is key to accurately locating points in this coordinate system.

In the study of polar coordinates, it's essential to understand that a single point can be represented by multiple ordered pairs. This concept is similar to coterminal angles in the unit circle, where angles like \( \frac{\pi}{6} \) and \( \frac{13\pi}{6} \) point to the same location. In polar coordinates, a point is defined by an ordered pair \( (r, \theta) \), where \( r \) is the radius and \( \theta \) is the angle. To find different representations of the same point, we can apply the same principles used for coterminal angles.

For any point represented as \( (r, \theta) \), we can generate additional ordered pairs by adding or subtracting multiples of \( 2\pi \) to the angle \( \theta \). This can be expressed mathematically as:

\( (r, \theta) \) is coterminal with \( (r, \theta + 2\pi n) \) for any integer \( n \).

Additionally, if we want to change the sign of \( r \) (making it negative), we must adjust the angle \( \theta \) by adding \( \pi \) to it. This ensures that the point remains in the same location. The relationship can be summarized as:

\( (r, \theta) \) is equivalent to \( (-r, \theta + \pi) \).

For example, starting with the point \( (4, \frac{\pi}{6}) \), we can find another representation by keeping \( r \) the same and adjusting \( \theta \). If we subtract \( 2\pi \) from \( \frac{\pi}{6} \), we get:

\( (4, \frac{\pi}{6} - 2\pi) = (4, -\frac{11\pi}{6}) \).

To find a representation with a negative \( r \), we set \( r = -4 \) and keep \( \theta \) within the interval \( [0, 2\pi] \). If we simply use \( \frac{\pi}{6} \), we find that it does not point to the same location. Instead, we must add \( \pi \) to \( \frac{\pi}{6} \) to get:

\( (-4, \frac{\pi}{6} + \pi) = (-4, \frac{7\pi}{6}) \).

By following these methods, we can generate an infinite number of ordered pairs for any given point in polar coordinates. This understanding is crucial for solving problems involving polar coordinates and helps in visualizing the relationships between different representations of the same point.

In this exercise, we explore the concept of polar coordinates, specifically focusing on the point represented by the coordinates \((-2, \frac{5\pi}{3})\). In polar coordinates, the first value represents the radius \(r\) and the second value represents the angle \(\theta\). Here, the negative radius indicates that we will plot the point in the opposite direction of the angle.

To begin, we identify the angle \(\theta = \frac{5\pi}{3}\). This angle is located in the fourth quadrant of the polar coordinate system. Since the radius \(r\) is negative, we move in the direction opposite to \(\frac{5\pi}{3}\), which results in the point being plotted at \((-2, \frac{5\pi}{3})\) or \((-2, -\frac{\pi}{3})\) when considering the equivalent angle in the standard position.

Next, we can generate additional sets of coordinates that represent the same point. One method to achieve this is by adding multiples of \(2\pi\) to the angle \(\theta\). For instance, adding \(2\pi\) to \(\frac{5\pi}{3}\) gives us:

\[\frac{5\pi}{3} + 2\pi = \frac{5\pi}{3} + \frac{6\pi}{3} = \frac{11\pi}{3}\]

This results in the coordinates \((-2, \frac{11\pi}{3})\), which still represents the same point in the polar coordinate system.

Continuing this process, we can add another \(2\pi\) to \(\frac{11\pi}{3}\):

\[\frac{11\pi}{3} + 2\pi = \frac{11\pi}{3} + \frac{6\pi}{3} = \frac{17\pi}{3}\]

This gives us a second set of coordinates \((-2, \frac{17\pi}{3})\), again representing the same point.

To find a third set of coordinates, we can change the radius \(r\) from negative to positive. When we do this, we must adjust the angle by adding \(\pi\) to the original angle. Thus, we take the original angle \(\frac{5\pi}{3}\) and add \(\pi\):

\[\frac{5\pi}{3} + \pi = \frac{5\pi}{3} + \frac{3\pi}{3} = \frac{8\pi}{3}\]

This results in the coordinates \((2, \frac{8\pi}{3})\), which also represents the same point in the polar coordinate system.

In summary, we have derived three sets of coordinates for the same point: \((-2, \frac{5\pi}{3})\), \((-2, \frac{11\pi}{3})\), and \((-2, \frac{17\pi}{3})\), as well as \((2, \frac{8\pi}{3})\). This illustrates the flexibility of polar coordinates, where multiple representations can describe the same location in the plane.