Back
BackProblem 1a
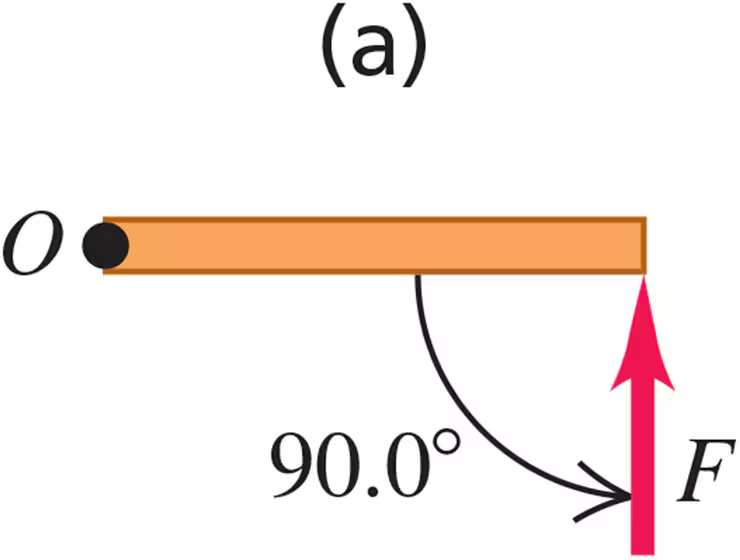
Calculate the torque (magnitude and direction) about point O due to the force F in each of the cases sketched in Fig. E10.1. In each case, both the force F and the rod lie in the plane of the page, the rod has length 4.00 m, and the force has magnitude F = 10.0 N.
Problem 5a
One force acting on a machine part is F = (-5.00 N)i + (4.00 N)j. The vector from the origin to the point where the force is applied is r = (-0.450 m)i +(0.150 m)j. In a sketch, show r, F, and the origin.
Problem 6a
A metal bar is in the -plane with one end of the bar at the origin. A force is applied to the bar at the point , . In terms of unit vectors and , what is the position vector for the point where the force is applied?
Problem 6b
A metal bar is in the -plane with one end of the bar at the origin. A force is applied to the bar at the point , . What are the magnitude and direction of the torque with respect to the origin produced by ?
Problem 7a
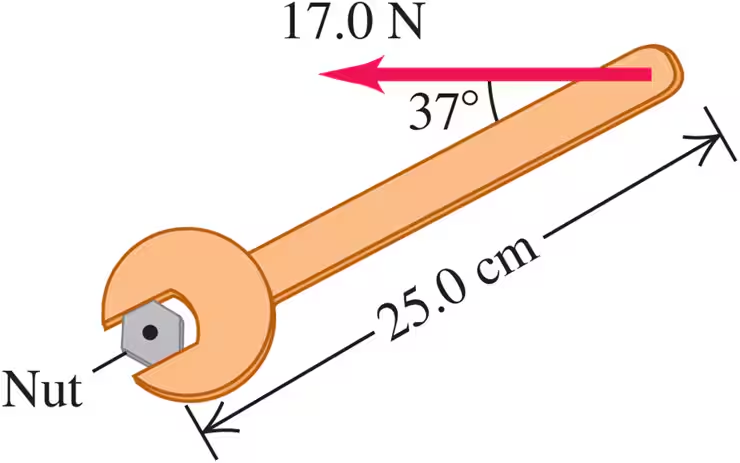
A machinist is using a wrench to loosen a nut. The wrench is 25.0 cm long, and he exerts a 17.0-N force at the end of the handle at 37° with the handle (Fig. E10.7). What torque does the machinist exert about the center of the nut?
Problem 7b
A machinist is using a wrench to loosen a nut. The wrench is 25.0 cm long, and he exerts a 17.0-N force at the end of the handle at 37° with the handle (Fig. E10.7). What is the maximum torque he could exert with this force, and how should the force be oriented?

Problem 9
The flywheel of an engine has moment of inertia 1.60 kg/m2 about its rotation axis. What constant torque is required to bring it up to an angular speed of 400 rev/min in 8.00 s, starting from rest?
Problem 10b
A cord is wrapped around the rim of a solid uniform wheel 0.250 m in radius and of mass 9.20 kg. A steady horizontal pull of 40.0 N to the right is exerted on the cord, pulling it off tangentially from the wheel. The wheel is mounted on frictionless bearings on a horizontal axle through its center. Find the magnitude and direction of the force that the axle exerts on the wheel.
Problem 10.4
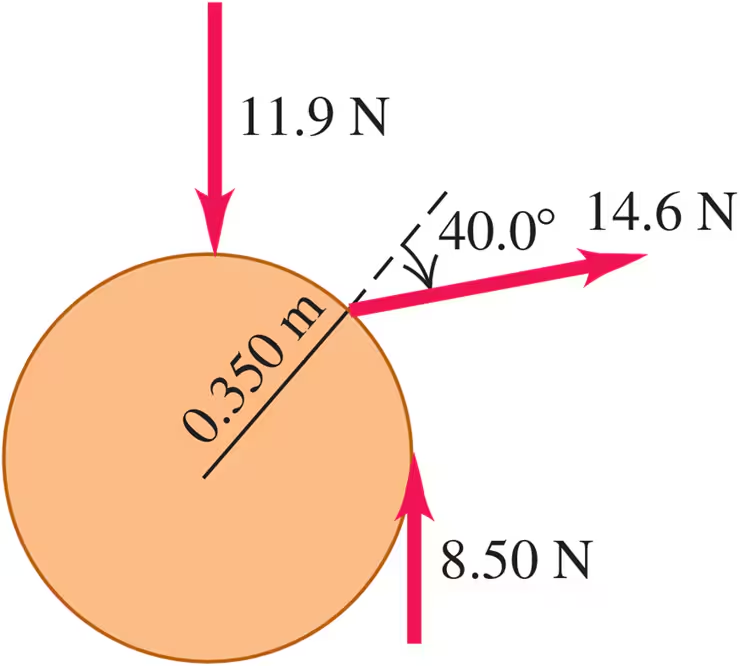
Three forces are applied to a wheel of radius 0.350 m, as shown in Fig. E10.4. One force is perpendicular to the rim, one is tangent to it, and the other one makes a 40.0° angle with the radius. What is the net torque on the wheel due to these three forces for an axis perpendicular to the wheel and passing through its center?
Problem 10.40a
(a) Calculate the magnitude of the angular momentum of the earth in a circular orbit around the sun. Is it reasonable to model it as a particle? Consult Appendix E and the astronomical data in Appendix F
Problem 11a
A machine part has the shape of a solid uniform sphere of mass 225 g and diameter 3.00 cm. It is spinning about a frictionless axle through its center, but at one point on its equator, it is scraping against metal, resulting in a friction force of 0.0200 N at that point. Find its angular acceleration.
Problem 11b
A machine part has the shape of a solid uniform sphere of mass 225 g and diameter 3.00 cm. It is spinning about a frictionless axle through its center, but at one point on its equator it is scraping against metal, resulting in a friction force of 0.0200 N at that point. How long will it take to decrease its rotational speed by 22.5 rad/s?
Problem 12a
A stone is suspended from the free end of a wire that is wrapped around the outer rim of a pulley, similar to what is shown in Fig. 10.10. The pulley is a uniform disk with mass 10.0 kg and radius 30.0 cm and turns on frictionless bearings. You measure that the stone travels 12.6 m in the first 3.00 s starting from rest. Find the mass of the stone.
Problem 12b
A stone is suspended from the free end of a wire that is wrapped around the outer rim of a pulley, similar to what is shown in Fig. 10.10. The pulley is a uniform disk with mass 10.0 kg and radius 30.0 cm and turns on frictionless bearings. You measure that the stone travels 12.6 m in the first 3.00 s starting from rest. Find the tension in the wire.
Problem 13a
A 2.00-kg textbook rests on a frictionless, horizontal surface. A cord attached to the book passes over a pulley whose diameter is 0.150 m, to a hanging book with mass 3.00 kg. The system is released from rest, and the books are observed to move 1.20 m in 0.800 s. What is the tension in each part of the cord?
Problem 14b
A 15.0-kg bucket of water is suspended by a very light rope wrapped around a solid uniform cylinder 0.300 m in diameter with mass 12.0 kg. The cylinder pivots on a frictionless axle through its center. The bucket is released from rest at the top of a well and falls 10.0 m to the water. With what speed does the bucket strike the water?
Problem 16b
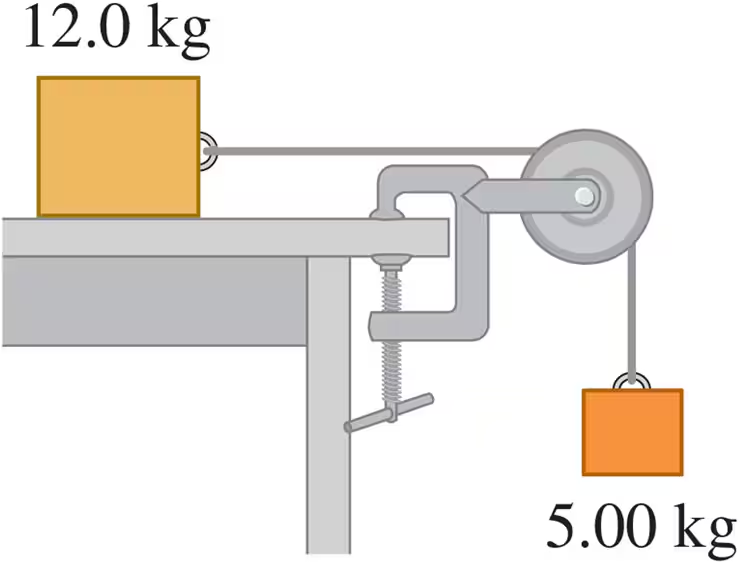
A 12.0-kg box resting on a horizontal, frictionless surface is attached to a 5.00-kg weight by a thin, light wire that passes over a frictionless pulley (Fig. E10.16). The pulley has the shape of a uniform solid disk of mass 2.00 kg and diameter 0.500 m. After the system is released, find the acceleration of the box.
Problem 19c
A 2.20-kg hoop 1.20 m in diameter is rolling to the right without slipping on a horizontal floor at a steady 2.60 rad/s. Find the velocity vector of each of the following points, as viewed by a person at rest on the ground: (i) the highest point on the hoop; (ii) the lowest point on the hoop; (iii) a point on the right side of the hoop, midway between the top and the bottom.
Problem 19d
A 2.20-kg hoop 1.20 m in diameter is rolling to the right without slipping on a horizontal floor at a steady 2.60 rad/s. Find the velocity vector for each of the points in part (c), but this time as viewed by someone moving along with the same velocity as the hoop.
Problem 23c
A solid ball is released from rest and slides down a hillside that slopes downward at 65.0° from the horizontal. In part (a), why did we use the coefficient of static friction and not the coefficient of kinetic friction?
Problem 33a
A playground merry-go-round has radius and moment of inertia about a vertical axle through its center, and it turns with negligible friction. A child applies an force tangentially to the edge of the merry-go-round for . If the merry-go-round is initially at rest, what is its angular speed after this interval?
Problem 33b
A playground merry-go-round has radius and moment of inertia about a vertical axle through its center, and it turns with negligible friction. A child applies an force tangentially to the edge of the merry-go-round for . If the merry-go-round is initially at rest, how much work did the child do on the merry-go-round?
Problem 34
An electric motor consumes 9.00 kJ of electrical energy in 1.00 min. If one-third of this energy goes into heat and other forms of internal energy of the motor, with the rest going to the motor output, how much torque will this engine develop if you run it at 2500 rpm?
Problem 35a
A 2.80-kg grinding wheel is in the form of a solid cylinder of radius 0.100 m. What constant torque will bring it from rest to an angular speed of 1200 rev/min in 2.5 s?
Problem 36e
An airplane propeller is 2.08 m in length (from tip to tip) and has a mass of 117 kg. When the airplane's engine is first started, it applies a constant torque of 1950 Nm to the propeller, which starts from rest. What is the instantaneous power output of the motor at the instant that the propeller has turned through 5.00 revolutions?
Problem 37a
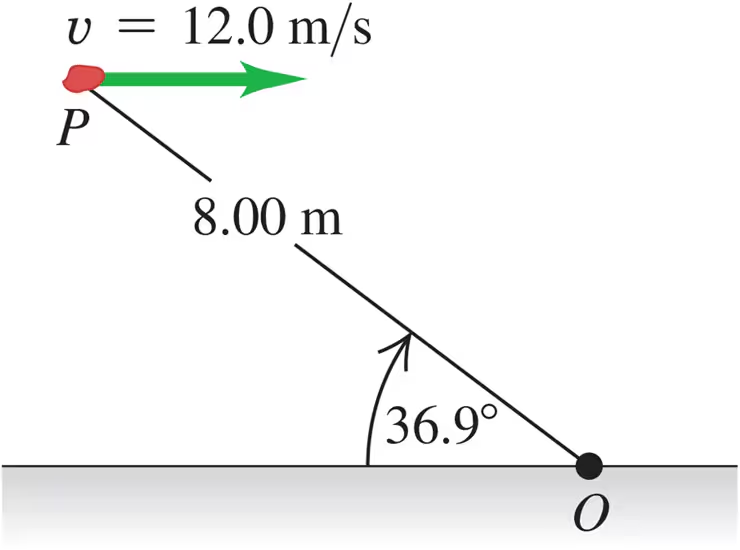
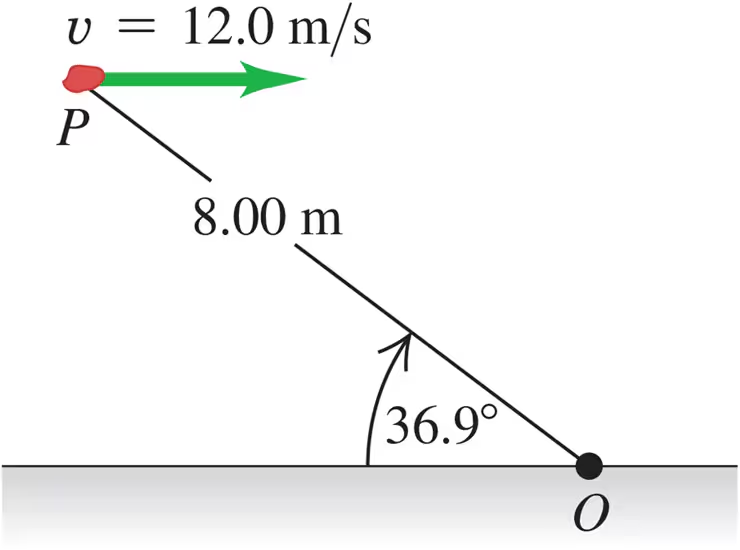
A 2.00-kg rock has a horizontal velocity of magnitude 12.0 m/s when it is at point P in Fig. E10.35. At this instant, what are the magnitude and direction of its angular momentum relative to point O?
Problem 37b
A 2.00-kg rock has a horizontal velocity of magnitude 12.0 m/s when it is at point P in Fig. E10.35. If the only force acting on the rock is its weight, what is the rate of change (magnitude and direction) of its angular momentum at this instant?
Problem 38
A woman with mass 50 kg is standing on the rim of a large disk that is rotating at 0.80 rev/s about an axis through its center. The disk has mass 110 kg and radius 4.0 m. Calculate the magnitude of the total angular momentum of the woman–disk system. (Assume that you can treat the woman as a point.)
Problem 41a
A hollow, thin-walled sphere of mass and diameter is rotating about an axle through its center. The angle (in radians) through which it turns as a function of time (in seconds) is given by , where A has numerical value and B has numerical value . What are the units of the constants A and B?
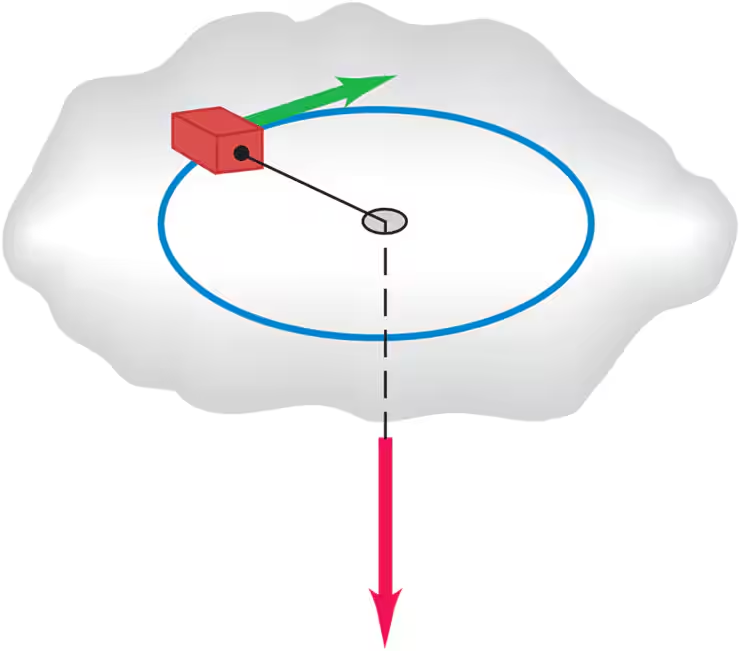
Problem 42a
A small block on a frictionless, horizontal surface has a mass of 0.0250 kg. It is attached to a massless cord passing through a hole in the surface (Fig. E10.40). The block is originally revolving at a distance of 0.300 m from the hole with an angular speed of 2.85 rad/s. The cord is then pulled from below, shortening the radius of the circle in which the block revolves to 0.150 m. Model the block as a particle. Is the angular momentum of the block conserved? Why or why not?