The angular velocity of a flywheel obeys the equation ω_z(t) = A + Bt², where t is in seconds and A and B are constants having numerical values 2.75 (for A) and 1.50 (for B). What is the angular acceleration of the wheel at (i) t = 0 and (ii) t = 5.00 s?

A fan blade rotates with angular velocity given by ω_z(t) = g - bt², where g = 5.00 rad/s and b = 0.800 rad/s³. Calculate the angular acceleration as a function of time.

A fan blade rotates with angular velocity given by ω_z(t) = g - bt², where g = 5.00 rad/s and b = 0.800 rad/s³. Calculate the instantaneous angular acceleration α_z at t = 3.00 s and the average angular acceleration α_av-z for the time interval t = 0 to t = 3.00 s. How do these two quantities compare? If they are different, why?

The angle θ through which a disk drive turns is given by θ(t) = a + bt - ct³, where a, b, and c are constants, t is in seconds, and θ is in radians. When t = 0, θ = π/4 rad and the angular velocity is 2.00 rad/s. When t = 1.50 s, the angular acceleration is 1.25 rad/s². Find a, b, and c, including their units.

The angle θ through which a disk drive turns is given by θ(t) = a + bt - ct³, where a, b, and c are constants, t is in seconds, and θ is in radians. When t = 0, θ = π/4 rad and the angular velocity is 2.00 rad/s. When t = 1.50 s, the angular acceleration is 1.25 rad/s². (b) What is the angular acceleration when θ = π/4 rad?

The angle θ through which a disk drive turns is given by θ(t) = a + bt - ct³, where a, b, and c are constants, t is in seconds, and θ is in radians. When t = 0, θ = π/4 rad and the angular velocity is 2.00 rad/s. When t = 1.50 s, the angular acceleration is 1.25 rad/s². What are θ and the angular velocity when the angular acceleration is 3.50 rad/s²?

A wheel is rotating about an axis that is in the z-direction. The angular velocity ω_z is -6.00 rad/s at t = 0, increases linearly with time, and is +4.00 rad/s at t = 7.00 s. We have taken counterclockwise rotation to be positive. Is the angular acceleration during this time interval positive or negative?

A wheel is rotating about an axis that is in the z-direction. The angular velocity ω_z is -6.00 rad/s at t = 0, increases linearly with time, and is +4.00 rad/s at t = 7.00 s. We have taken counterclockwise rotation to be positive. During what time interval is the speed of the wheel increasing? Decreasing?

A wheel is rotating about an axis that is in the z-direction. The angular velocity ω_z is -6.00 rad/s at t = 0, increases linearly with time, and is +4.00 rad/s at t = 7.00 s. We have taken counterclockwise rotation to be positive. What is the angular displacement of the wheel at t = 7.00 s?

A bicycle wheel has an initial angular velocity of 1.50 rad/s. (a) If its angular acceleration is constant and equal to 0.200 rad/s², what is its angular velocity at t = 2.50 s? (b) Through what angle has the wheel turned between t = 0 and t = 2.50 s?

An electric fan is turned off, and its angular velocity decreases uniformly from 500 rev/min to 200 rev/min in 4.00 s. Find the angular acceleration in rev/s² and the number of revolutions made by the motor in the 4.00-s interval.

An electric fan is turned off, and its angular velocity decreases uniformly from 500 rev/min to 200 rev/min in 4.00 s. How many more seconds are required for the fan to come to rest if the angular acceleration remains constant at the value calculated in part (a)?

A high-speed flywheel in a motor is spinning at 500 rpm when a power failure suddenly occurs. The flywheel has mass 40.0 kg and diameter 75.0 cm. The power is off for 30.0 s, and during this time the flywheel slows due to friction in its axle bearings. During the time the power is off, the flywheel makes 200 complete revolutions. At what rate is the flywheel spinning when the power comes back on?

A compact disc (CD) stores music in a coded pattern of tiny pits 10^-7 m deep. The pits are arranged in a track that spirals outward toward the rim of the disc; the inner and outer radii of this spiral are 25.0 mm and 58.0 mm, respectively. As the disc spins inside a CD player, the track is scanned at a constant linear speed of 1.25 m/s. What is the angular speed of the CD when the innermost part of the track is scanned? The outermost part of the track?

CA compact disc (CD) stores music in a coded pattern of tiny pits 10-7 m deep. The pits are arranged in a track that spirals outward toward the rim of the disc; the inner and outer radii of this spiral are 25.0 mm and 58.0 mm, respectively. As the disc spins inside a CD player, the track is scanned at a constant linear speed of 1.25 m/s. The maximum playing time of a CD is 74.0 min. What would be the length of the track on such a maximum-duration CD if it were stretched out in a straight line?

A compact disc (CD) stores music in a coded pattern of tiny pits 10^-7 m deep. The pits are arranged in a track that spirals outward toward the rim of the disc; the inner and outer radii of this spiral are 25.0 mm and 58.0 mm, respectively. As the disc spins inside a CD player, the track is scanned at a constant linear speed of 1.25 m/s. What is the average angular acceleration of a maximum duration CD during its 74.0-min playing time? Take the direction of rotation of the disc to be positive.

A wheel of diameter 40.0 cm starts from rest and rotates with a constant angular acceleration of 3.00 rad/s². Compute the radial acceleration of a point on the rim for the instant the wheel completes its second revolution from the relationship a_rad = ω²r.

A wheel of diameter 40.0 cm starts from rest and rotates with a constant angular acceleration of 3.00 rad/s². Compute the radial acceleration of a point on the rim for the instant the wheel completes its second revolution from the relationship a_rad = v²/r.

An electric turntable 0.750 m in diameter is rotating about a fixed axis with an initial angular velocity of 0.250 rev/s and a constant angular acceleration of 0.900 rev/s².

(a) Compute the angular velocity of the turntable after 0.200 s.

(b) Through how many revolutions has the turntable spun in this time interval?

An electric turntable 0.750 m in diameter is rotating about a fixed axis with an initial angular velocity of 0.250 rev/s and a constant angular acceleration of 0.900 rev/s². What is the tangential speed of a point on the rim of the turntable at t = 0.200 s?

An electric turntable 0.750 m in diameter is rotating about a fixed axis with an initial angular velocity of 0.250 rev/s and a constant angular acceleration of 0.900 rev/s². What is the magnitude of the resultant acceleration of a point on the rim at t = 0.200 s?

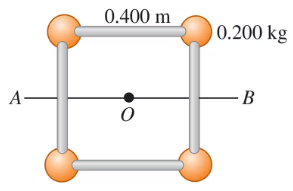
Four small spheres, each of which you can regard as a point of mass 0.200 kg, are arranged in a square 0.400 m on a side and connected by extremely light rods (Fig. E9.28). Find the moment of inertia of the system about an axis that passes through the centers of the upper left and lower right spheres and through point O.

Calculate the moment of inertia of each of the following uniform objects about the axes indicated. Consult Table 9.2 as needed. A thin 2.50-kg rod of length 75.0 cm, about an axis perpendicular to it and passing through (i) one end and (ii) its center, and (iii) about an axis parallel to the rod and passing through it.

A uniform bar has two small balls glued to its ends. The bar is 2.00 m long and has mass 4.00 kg, while the balls each have mass 0.300 kg and can be treated as point masses. Find the moment of inertia of this combination about an axis perpendicular to the bar through its center;

A uniform bar has two small balls glued to its ends. The bar is 2.00 m long and has mass 4.00 kg, while the balls each have mass 0.300 kg and can be treated as point masses. Find the moment of inertia of this combination about an axis perpendicular to the bar through one of the balls;

A uniform bar has two small balls glued to its ends. The bar is 2.00 m long and has mass 4.00 kg, while the balls each have mass 0.300 kg and can be treated as point masses. Find the moment of inertia of this combination about an axis parallel to the bar through both balls;

A uniform bar has two small balls glued to its ends. The bar is 2.00 m long and has mass 4.00 kg, while the balls each have mass 0.300 kg and can be treated as point masses. Find the moment of inertia of this combination about an axis parallel to the bar and 0.500 m from it.

You are a project manager for a manufacturing company. One of the machine parts on the assembly line is a thin, uniform rod that is 60.0 cm long and has mass 0.400 kg. What is the moment of inertia of this rod for an axis at its center, perpendicular to the rod?

You are a project manager for a manufacturing company. One of the machine parts on the assembly line is a thin, uniform rod that is 60.0 cm long and has mass 0.400 kg. One of your engineers has proposed to reduce the moment of inertia by bending the rod at its center into a V-shape, with a 60.0^o angle at its vertex. What would be the moment of inertia of this bent rod about an axis perpendicular to the plane of the V at its vertex?

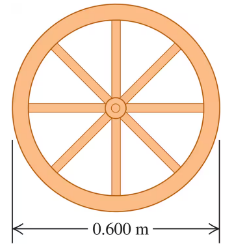
A wagon wheel is constructed as shown in Fig. E9.33. The radius of the wheel is 0.300 m, and the rim has mass 1.40 kg. Each of the eight spokes that lie along a diameter and are 0.300 m long has mass 0.280 kg. What is the moment of inertia of the wheel about an axis through its center and perpendicular to the plane of the wheel? (Use Table 9.2.)