Back
BackProblem 26d
A box of bananas weighing N rests on a horizontal surface. The coefficient of static friction between the box and the surface is , and the coefficient of kinetic friction is . What minimum horizontal force must the monkey apply to keep the box moving at constant velocity once it has been started?
Problem 26e
A box of bananas weighing N rests on a horizontal surface. The coefficient of static friction between the box and the surface is , and the coefficient of kinetic friction is . If the monkey applies a horizontal force of N, what is the magnitude of the friction force and what is the box's acceleration?
Problem 27a
A -kg crate of tools rests on a horizontal floor. You exert a gradually increasing horizontal push on it, and the crate just begins to move when your force exceeds N. Then you must reduce your push to N to keep it moving at a steady cm/s. What are the coefficients of static and kinetic friction between the crate and the floor?
Problem 27b
A -kg crate of tools rests on a horizontal floor. You exert a gradually increasing horizontal push on it, and the crate just begins to move when your force exceeds N. Then you must reduce your push to N to keep it moving at a steady cm/s. What push must you exert to give it an acceleration of m/s2?
Problem 27c
A -kg crate of tools rests on a horizontal floor. You exert a gradually increasing horizontal push on it, and the crate just begins to move when your force exceeds N. Then you must reduce your push to N to keep it moving at a steady cm/s. Suppose you were performing the same experiment on the moon, where the acceleration due to gravity is m/s2.
(i) What magnitude push would cause it to move?
(ii) What would its acceleration be if you maintained the push in part (b)? Note: Part (b) asked what push you must exert to give it an acceleration of m/s2.
Problem 32
A pickup truck is carrying a toolbox, but the rear gate of the truck is missing. The toolbox will slide out if it is set moving. The coefficients of kinetic friction and static friction between the box and the level bed of the truck are and , respectively. Starting from rest, what is the shortest time this truck could accelerate uniformly to m/s without causing the box to slide? Draw a free-body diagram of the toolbox.
Problem 36b
A -kg box of textbooks rests on a loading ramp that makes an angle with the horizontal. The coefficient of kinetic friction is , and the coefficient of static friction is . At this angle, find the acceleration once the box has begun to move.
Problem 37a
Two crates connected by a rope lie on a horizontal surface (Fig. E). Crate A has mass , and crate B has mass . The coefficient of kinetic friction between each crate and the surface is . The crates are pulled to the right at constant velocity by a horizontal force . Draw one or more free-body diagrams to calculate the following in terms of , , and : the magnitude of .

Problem 37b
Two crates connected by a rope lie on a horizontal surface (Fig. E). Crate A has mass , and crate B has mass . The coefficient of kinetic friction between each crate and the surface is . The crates are pulled to the right at constant velocity by a horizontal force . Draw one or more free-body diagrams to calculate the following in terms of , , and : the tension in the rope connecting the blocks.

Problem 40a
You throw a baseball straight upward. The drag force is proportional to . In terms of , what is the -component of the ball's acceleration when the ball's speed is half its terminal speed and it is moving up?
Problem 40b
You throw a baseball straight upward. The drag force is proportional to . In terms of , what is the -component of the ball's acceleration when the ball's speed is half its terminal speed and it is moving back down?
Problem 44b
A -kg ice skater spins about a vertical axis through her body with her arms horizontally outstretched; she makes turns each second. The distance from one hand to the other is m. Biometric measurements indicate that each hand typically makes up about of body weight. What horizontal force must her wrist exert on her hand?
Problem 45a
A small remote-controlled car with mass kg moves at a constant speed of m/s in a track formed by a vertical circle inside a hollow metal cylinder that has a radius of m (Fig. E). What is the magnitude of the normal force exerted on the car by the walls of the cylinder at point (bottom of the track)?

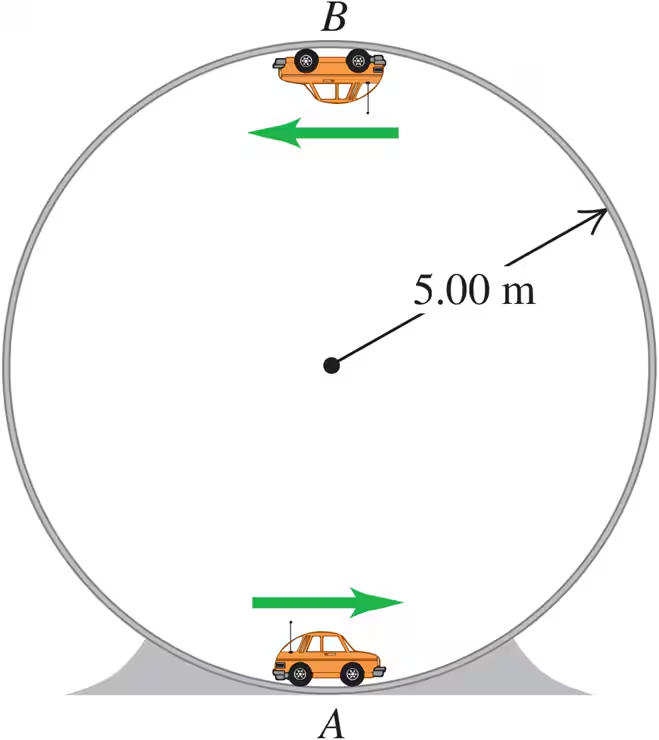
Problem 45b
A small remote-controlled car with mass kg moves at a constant speed of m/s in a track formed by a vertical circle inside a hollow metal cylinder that has a radius of m (Fig. E). What is the magnitude of the normal force exerted on the car by the walls of the cylinder at point (top of the track)?

Problem 46
A small car with mass kg travels at constant speed on the inside of a track that is a vertical circle with radius m (Fig. E). If the normal force exerted by the track on the car when it is at the top of the track (point ) is N, what is the normal force on the car when it is at the bottom of the track (point )?
Problem 48a
A flat (unbanked) curve on a highway has a radius of m. A car rounds the curve at a speed of m/s. What is the minimum coefficient of static friction that will prevent sliding?
Problem 49a
A -kg car and a -kg pickup truck approach a curve on a highway that has a radius of m. At what angle should the highway engineer bank this curve so that vehicles traveling at mi/h can safely round it regardless of the condition of their tires? Should the heavy truck go slower than the lighter car?
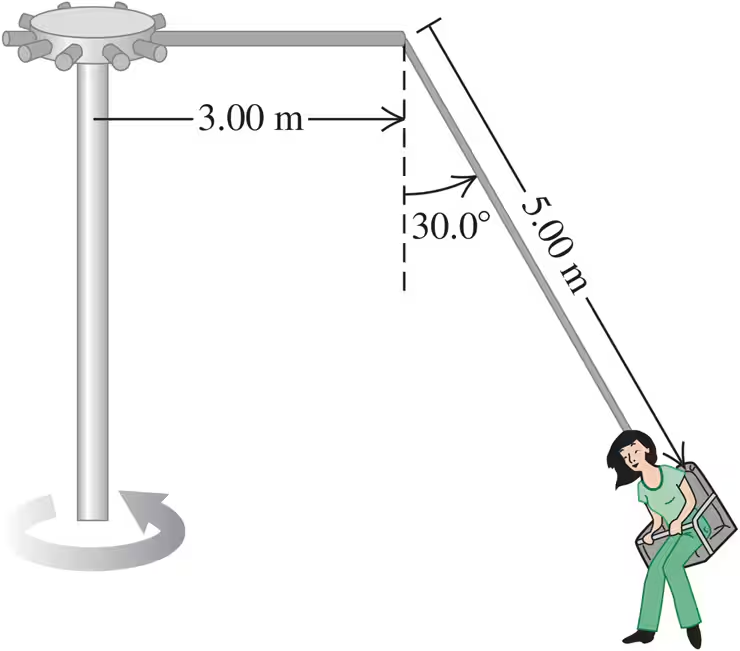
Problem 50a
The 'Giant Swing' at a county fair consists of a vertical central shaft with a number of horizontal arms attached at its upper end. Each arm supports a seat suspended from a cable m long, and the upper end of the cable is fastened to the arm at a point m from the central shaft (Fig. E). Find the time of one revolution of the swing if the cable supporting a seat makes an angle of with the vertical.
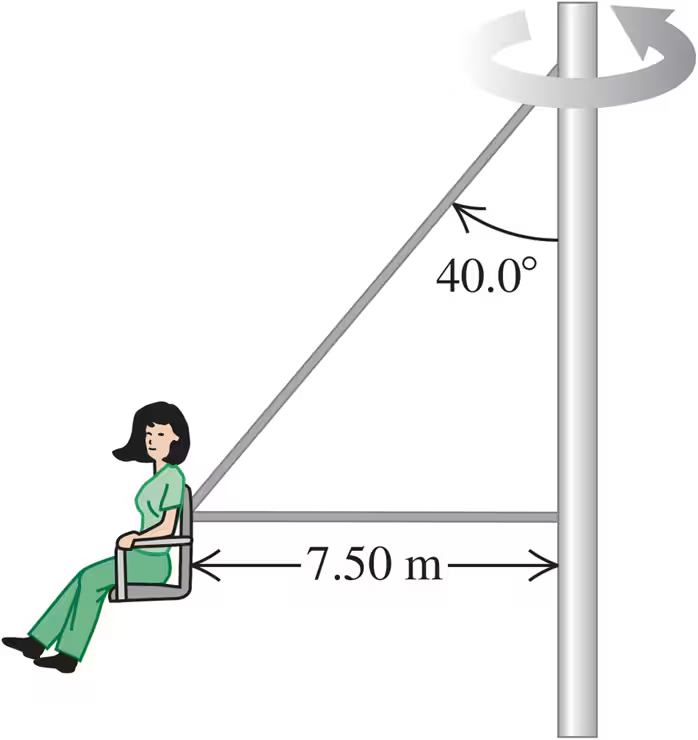
Problem 51
In another version of the 'Giant Swing' (see Exercise ), the seat is connected to two cables, one of which is horizontal (Fig. E). The seat swings in a horizontal circle at a rate of rpm (rev/min). If the seat weighs N and an -N person is sitting in it, find the tension in each cable.
Problem 53a
One problem for humans living in outer space is that they are apparently weightless. One way around this problem is to design a space station that spins about its center at a constant rate. This creates 'artificial gravity' at the outside rim of the station. If the diameter of the space station is m, how many revolutions per minute are needed for the 'artificial gravity' acceleration to be m/s2?
Problem 54a
The Cosmo Clock 21 Ferris wheel in Yokohama, Japan, has a diameter of m. Its name comes from its arms, each of which can function as a second hand (so that it makes one revolution every s). Find the speed of the passengers when the Ferris wheel is rotating at this rate.
Problem 54b
The Cosmo Clock 21 Ferris wheel in Yokohama, Japan, has a diameter of m. Its name comes from its arms, each of which can function as a second hand (so that it makes one revolution every s). A passenger weighs N at the weight-guessing booth on the ground. What is his apparent weight at the highest and at the lowest point on the Ferris wheel?
Problem 54c
The Cosmo Clock 21 Ferris wheel in Yokohama, Japan, has a diameter of m. Its name comes from its arms, each of which can function as a second hand (so that it makes one revolution every s). What would be the time for one revolution if the passenger's apparent weight at the highest point were zero?
Problem 54d
The Cosmo Clock 21 Ferris wheel in Yokohama, Japan, has a diameter of m. Its name comes from its arms, each of which can function as a second hand (so that it makes one revolution every s). What then would be the passenger's apparent weight at the lowest point?