An electron is moving as a free particle in the $-x$-direction with momentum that has magnitude $4.50\times {10}^{-24}$ kg-m/s. What is the one-­dimensional time-­dependent wave function of the electron?

A free particle moving in one dimension has wave function $\psi (x,t)=A[e^{i(kx-\omega t)}-e^{i(2kx-4\omega t)}]$ where $k$ and $v$ are positive real constants.

(a) At $t=0$, what are the two smallest positive values of $x$ for which the probability function $\mid \psi (x,t){\mid }^2$ is a maximum?

(b) Repeat part (a) for time $t=\frac{2\pi }{\omega }$.

An electron is moving as a free particle in the $-x$-direction with momentum that has magnitude $4.50\times {10}^{-24}$ kg*m/s. Let $k_2=3k_1=3k$. At $t=0$, the probability distribution func­tion $\mid \Psi (x,t){\mid }^2$ has a maximum at $x=0$.

(a) What is the smallest positive value of $x$ for which the probability distribution function has a maximum at time $t=\frac{2\pi }{\omega }$, where $\omega =h{k}^2/2m$?

(b) From your result in part (a), what is the average speed with which the probability distribution is moving in the $+x$­-direction?

A particle is described by a wave function $\psi \left(x\right)=A{e}^{-\alpha x^2}$, where $A$ and $\alpha$ are real, positive constants. If the value of $\alpha$ is increased, what effect does this have on (a) the particle’s uncer­tainty in position and (b) the particle’s uncertainty in momentum? Explain your answers.

Consider a wave function given by $\psi \left(x\right)=Asin\text{⁡}kx$, where $k=2\pi /\lambda$ and $A$ is a real constant.

(a) For what values of $x$ is there the highest probability of finding the particle described by this wave function? Explain.

(b) For which values of $x$ is the probability zero? Explain.

Let ${\psi }_1$ and ${\psi }_2$ be two solutions of Eq. ($40.23$) [$-\frac{h^2}{2m}\frac{d^2\psi \left(x\right)}{d{x}^2}+U\left(x\right)\psi \left(x\right)=E\psi \left(x\right)$] with energies $E_1$ and $E_2$ respectively, where $E_1\ne E_2$. Is $\psi =A{\psi }_1+B{\psi }_2$, where $A$ and $B$ are nonzero constants, a solution to Eq. ($40.23$)? Explain your answer.

(a) Find the lowest energy level for a particle in a box if the particle is a billiard ball ($m=0.20$ kg) and the box has a width of $1.3$ m, the size of a billiard table. (Assume that the billiard ball slides without friction rather than rolls; that is, ignore the rotational kinetic energy.)

(b) Since the energy in part (a) is all kinetic, to what speed does this correspond? How much time would it take at this speed for the ball to move from one side of the table to the other?

A particle in a box is a billiard ball ($m = 0.20$ kg) and the box has a width of $1.3$ m, the size of a billiard table. (Assume that the billiard ball slides without friction rather than rolls; that is, ignore the rotational kinetic energy.) What is the difference in energy between the $n=2$ and $n=1$ levels? Are quantum­ mechanical effects important for the game of billiards?

A proton is in a box of width $L$. What must the width of the box be for the ground­-level energy to be $5.0$ MeV, a typi­cal value for the energy with which the particles in a nucleus are bound? Compare your result to the size of a nucleus — that is, on the order of ${10}^{-14}$ m.

When a hydrogen atom undergoes a transition from the $n=2$ to the $n=1$ level, a photon with $\lambda =122$ nm is emitted.

(a) If the atom is modeled as an electron in a one-­dimensional box, what is the width of the box in order for the $n=2$ to $n=1$ transi­tion to correspond to emission of a photon of this energy?

(b) For a box with the width calculated in part (a), what is the ground­ state energy? How does this correspond to the ground ­state energy of a hydrogen atom?

(c) Do you think a one­-dimensional box is a good model for a hydrogen atom? Explain. (Hint: Compare the spacing between adjacent energy levels as a function of $n$.)

An electron in a one­-dimensional box has ground ­state energy $2.00$ eV. What is the wavelength of the photon absorbed when the electron makes a transition to the second excited state?

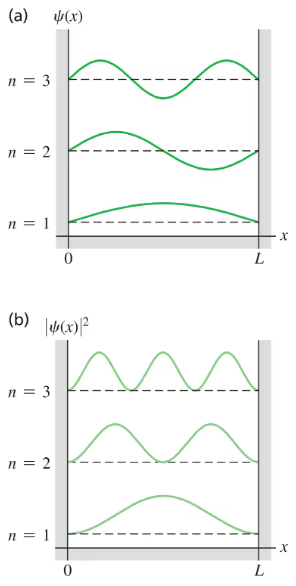
Recall that $\left(\mid \psi {\mid }^2\right)dx$ is the probability of finding the par­ticle that has normalized wave function $\psi \left(x\right)$ in the interval $x$ to $x+dx$. Consider a particle in a box with rigid walls at $x=0$ and $x=L$. Let the particle be in the ground level and use ${\psi }_n$ as given in Eq. ($40.35$) ${\psi }_n\left(x\right)=\sqrt{\frac{2}{L}}sin\text{⁡}\left[\right(\frac{n\pi x}{L}\left)\right]$ where $n=1,2,3,\dots$.

(a) For which values of $x$, if any, in the range from $0$ to $L$ is the probability of finding the particle zero?

(b) For which values of $x$ is the probability highest?

(c) In parts (a) and (b) are your answers consistent with Fig. $40.12$? Explain.

(a) Find the excitation energy from the ground level to the third excited level for an electron confined to a box of width $0.360$ nm.

(b) The electron makes a transition from the $n=1$ to $n=4$ level by absorbing a photon. Calculate the wave­length of this photon.

An electron is in a box of width $3.0\times {10}^{-10}$ m. What are the de Broglie wavelength and the magnitude of the momentum of the electron if it is in (a) the $n=1$ level; (b) the $n=2$ level; (c) the $n=3$ level? In each case how does the wavelength compare to the width of the box?

(a) An electron with initial kinetic energy $32$ eV encoun­ters a square barrier with height $41$ eV and width $0.25$ nm. What is the probability that the electron will tunnel through the barrier?

(b) A proton with the same kinetic energy encounters the same barrier. What is the probability that the proton will tunnel through the barrier?

An electron with initial kinetic energy $6.0$ eV encounters a barrier with height $11.0$ eV. What is the probability of tunneling if the width of the barrier is (a) $0.80$ nm and (b) $0.40$ nm?

An electron with initial kinetic energy $5.0$ eV encoun­ters a barrier with height $U_0$ and width $0.60$ nm. What is the transmission coefficient if (a) $U_0=7.0$ eV; (b) $U_0=9.0$ eV; (c) $U_0=13.0$ eV?

While undergoing a transition from the $n=1$ to the $n=2$ energy level, a harmonic oscillator absorbs a photon of wavelength $6.50$ $\mu$m. What is the wavelength of the absorbed photon when this oscillator undergoes a transition (a) from the $n=2$ to the $n=3$ energy level and (b) from the $n=1$ to the $n=3$ energy level?

(c) What is the value of $\sqrt{\left(k^{\prime }/m\right)}$, the angular oscillation frequency of the corresponding Newtonian oscillator?

For the ground level of a harmonic oscillator, $\text{∆}x\text{∆}{p}_x=\text{ħ}/2$. Do a similar analysis for an excited level that has quantum number $$$n$. How does the uncer­tainty product $\text{∆}x\text{∆}{p}_x$ depend on $n$?

An electron is in a box of width 3.0*10^-10 m. What are the de Broglie wavelength and the magnitude of the momentum of the electron if it is in (a) the n = 1 level; (b) the n = 2 level; (c) the n = 3 level? In each case how does the wavelength compare to the width of the box?

A free particle moving in one dimension has wave function ψ(x,t) = A[e^i(kx-ωt) -e^i(2kx-4ωt)] where k and v are positive real constants. (c) Calculate v_av as the distance the maxima have moved divided by the elapsed time.