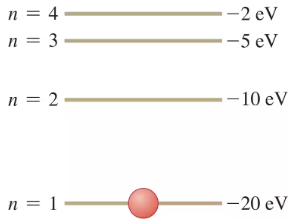Back
BackProblem 1
(a) An electron moves with a speed of m/s. What is its de Broglie wavelength?
(b) A proton moves with the same speed. Determine its de Broglie wavelength.
Problem 2a
For crystal diffraction experiments (discussed in Section ), wavelengths on the order of nm are often appropriate. Find the energy in electron volts for a particle with this wavelength if the particle is a photon.
Problem 3
An electron has a de Broglie wavelength of m. Determine (a) the magnitude of its momentum and (b) its kinetic energy (in joules and in electron volts).
Problem 4
An alpha particle ( kg) emitted in the radioactive decay of uranium- has an energy of MeV. What is its de Broglie wavelength?
Problem 5
An electron is moving with a speed of m/s. What is the speed of a proton that has the same de Broglie wavelength as this electron?
Problem 9
Calculate the de Broglie wavelength of a -g bullet that is moving at m/s. Will the bullet exhibit wavelike properties?
Problem 10
Through what potential difference must electrons be accelerated if they are to have:
(a) the same wavelength as an x ray of wavelength nm; and
(b) the same energy as the x ray in part (a)?
Problem 16
A -MeV alpha particle from a Ra decay makes a head-on collision with a uranium nucleus. A uranium nucleus has protons.
(a) What is the distance of closest approach of the alpha particle to the center of the nucleus? Assume that the uranium nucleus remains at rest and that the distance of closest approach is much greater than the radius of the uranium nucleus.
(b) What is the force on the alpha particle at the instant when it is at the distance of closest approach?
Problem 17
A beam of alpha particles is incident on a target of lead. A particular alpha particle comes in 'head-on' to a particular lead nucleus and stops m away from the center of the nucleus. (This point is well outside the nucleus.) Assume that the lead nucleus, which has protons, remains at rest. The mass of the alpha particle is kg.
(a) Calculate the electrostatic potential energy at the instant that the alpha particle stops. Express your result in joules and in MeV.
(b) What initial kinetic energy (in joules and in MeV) did the alpha particle have?
(c) What was the initial speed of the alpha particle?
Problem 19
A hydrogen atom is in a state with energy eV. In the Bohr model, what is the angular momentum of the electron in the atom, with respect to an axis at the nucleus?
Problem 21a
A triply ionized beryllium ion, Be3+ (a beryllium atom with three electrons removed), behaves very much like a hydrogen atom except that the nuclear charge is four times as great. What is the ground-level energy of Be3+? How does this compare to the ground-level energy of the hydrogen atom?
Problem 21c
A triply ionized beryllium ion, Be3+ (a beryllium atom with three electrons removed), behaves very much like a hydrogen atom except that the nuclear charge is four times as great. For the hydrogen atom, the wavelength of the photon emitted in the to transition is nm (see Example ). What is the wavelength of the photon emitted when a Be3+ ion undergoes this transition?
Problem 25b
The energy-level scheme for the hypothetical one-electron element Searsium is shown in Fig. . The potential energy is taken to be zero for an electron at an infinite distance from the nucleus. An -eV photon is absorbed by a Searsium atom in its ground level. As the atom returns to its ground level, what possible energies can the emitted photons have? Assume that there can be transitions between all pairs of levels.
Problem 27a
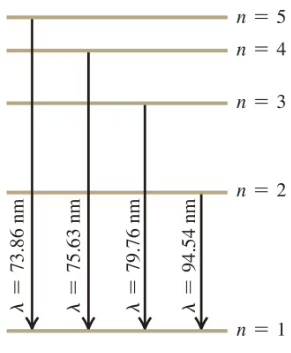
In a set of experiments on a hypothetical one-electron atom, you measure the wavelengths of the photons emitted from transitions ending in the ground level (), as shown in the energy-level diagram in Fig. E. You also observe that it takes eV to ionize this atom. What is the energy of the atom in each of the levels (, , etc.) shown in the figure?
Problem 28
Find the longest and shortest wavelengths in the Lyman and Paschen series for hydrogen. In what region of the electromagnetic spectrum does each series lie?
Problem 30
Use Balmer's formula to calculate (a) the wavelength, (b) the frequency, and (c) the photon energy for the Hg line of the Balmer series for hydrogen.
Problem 31
Using a mixture of CO2, N2, and sometimes He, CO2 lasers emit a wavelength of m. At power of kW, such lasers are used for surgery. How many photons per second does a CO2 laser deliver to the tissue during its use in an operation?
Problem 33
How many photons per second are emitted by a -mW CO2 laser that has a wavelength of mm?
Problem 34c
Photorefractive keratectomy (PRK) is a laser-based surgical procedure that corrects near- and farsightedness by removing part of the lens of the eye to change its curvature and hence focal length. This procedure can remove layers mm thick using pulses lasting ns from a laser beam of wavelength nm. Low-intensity beams can be used because each individual photon has enough energy to break the covalent bonds of the tissue. If a -mW beam is used, how many photons are delivered to the lens in each pulse?
Problem 40
The shortest visible wavelength is about nm. What is the temperature of an ideal radiator whose spectral emittance peaks at this wavelength?
Problem 41
Two stars, both of which behave like ideal blackbodies, radiate the same total energy per second. The cooler one has a surface temperature and a diameter times that of the hotter star.
(a) What is the temperature of the hotter star in terms of ?
(b) What is the ratio of the peak-intensity wavelength of the hot star to the peak-intensity wavelength of the cool star?
Problem 44
A pesky -mg mosquito is annoying you as you attempt to study physics in your room, which is m wide and m high. You decide to swat the bothersome insect as it flies toward you, but you need to estimate its speed to make a successful hit.
(a) What is the maximum uncertainty in the horizontal position of the mosquito?
(b) What limit does the Heisenberg uncertainty principle place on your ability to know the horizontal velocity of this mosquito? Is this limitation a serious impediment to your attempt to swat it?
Problem 45a
The uncertainty in the y-component of a proton's position is m. What is the minimum uncertainty in a simultaneous measurement of the -component of the proton's velocity?
Problem 46
-g marble is gently placed on a horizontal tabletop that is m wide.
(a) What is the maximum uncertainty in the horizontal position of the marble?
(b) According to the Heisenberg uncertainty principle, what is the minimum uncertainty in the horizontal velocity of the marble?
(c) In light of your answer to part (b), what is the longest time the marble could remain on the table? Compare this time to the age of the universe, which is approximately billion years. (Hint: Can you know that the horizontal velocity of the marble is exactly zero?)
Problem 47
A scientist has devised a new method of isolating individual particles. He claims that this method enables him to detect simultaneously the position of a particle along an axis with a standard deviation of nm and its momentum component along this axis with a standard deviation of kg-m/s. Use the Heisenberg uncertainty principle to evaluate the validity of this claim.
Problem 48
(a) The -coordinate of an electron is measured with an uncertainty of mm. What is the x-component of the electron's velocity, , if the minimum percent uncertainty in a simultaneous measurement of is ?
(b) Repeat part (a) for a proton.