Back
BackProblem 1
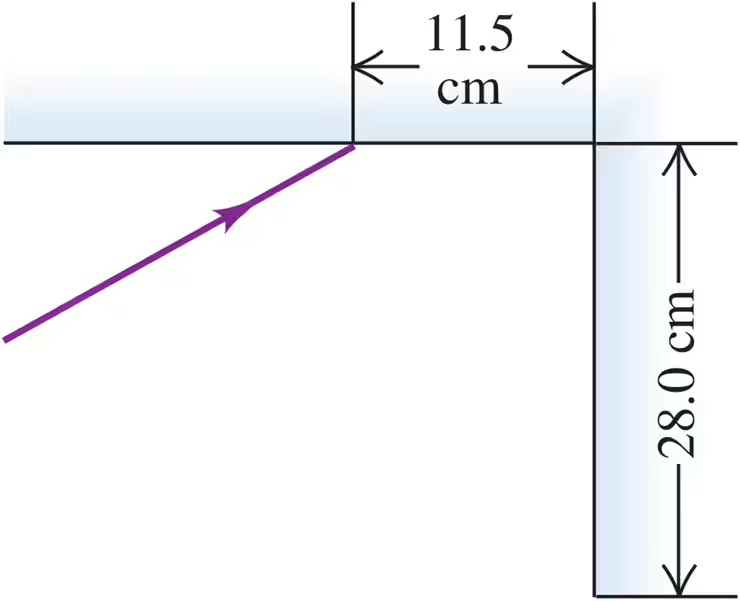
Two plane mirrors intersect at right angles. A laser beam strikes the first of them at a point 11.5 cm from their point of intersection, as shown in Fig. E33.1. For what angle of incidence at the first mirror will this ray strike the midpoint of the second mirror (which is 28.0 cm long) after reflecting from the first mirror?
Problem 3b
A beam of light has a wavelength of 650 nm in vacuum. What is the wavelength of these waves in the liquid?
Problem 5b
A light beam travels at 1.94 × 108 m/s in quartz. The wavelength of the light in quartz is 355 nm. If this same light travels through air, what is its wavelength there?
Problem 6
Light of a certain frequency has a wavelength of 526 nm in water. What is the wavelength of this light in benzene?
Problem 9
Light traveling in air is incident on the surface of a block of plastic at an angle of 62.7° to the normal and is bent so that it makes a 48.1° angle with the normal in the plastic. Find the speed of light in the plastic.
Problem 10
(a) A tank containing methanol has walls 2.50 cm thick made of glass of refractive index 1.550. Light from the outside air strikes the glass at a 41.3° angle with the normal to the glass. Find the angle the light makes with the normal in the methanol. (b) The tank is emptied and refilled with an unknown liquid. If light incident at the same angle as in part (a) enters the liquid in the tank at an angle of 20.2° from the normal, what is the refractive index of the unknown liquid?
Problem 11b
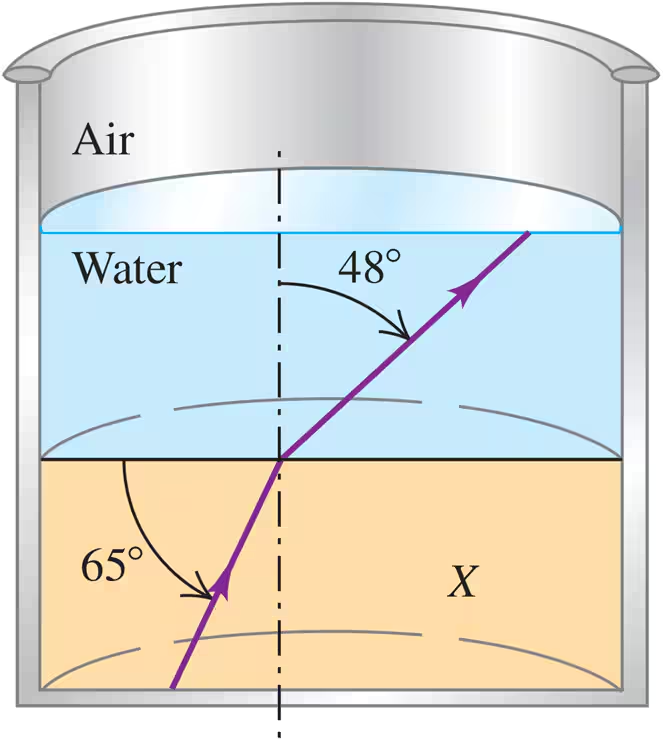
As shown in Fig. E33.11, a layer of water covers a slab of material X in a beaker. A ray of light traveling upward follows the path indicated. Using the information on the figure, find the angle the light makes with the normal in the air.
Problem 12a
A horizontal, parallel-sided plate of glass having a refractive index of 1.52 is in contact with the surface of water in a tank. A ray coming from above in air makes an angle of incidence of 35.0° with the normal to the top surface of the glass. What angle does the ray refracted into the water make with the normal to the surface?
Problem 15a
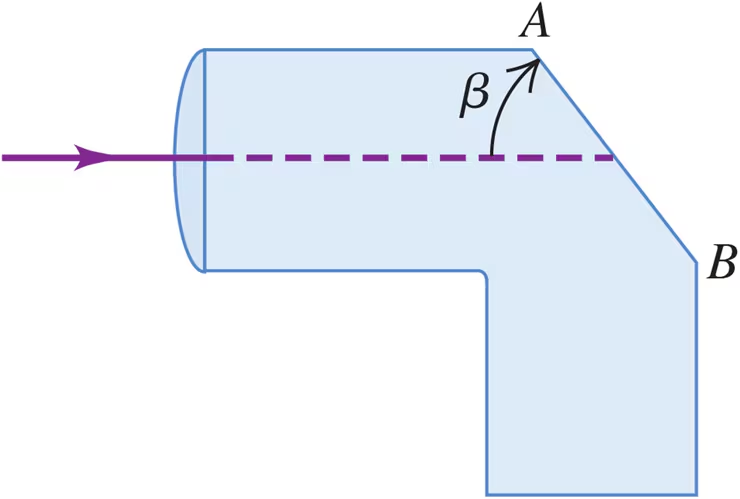
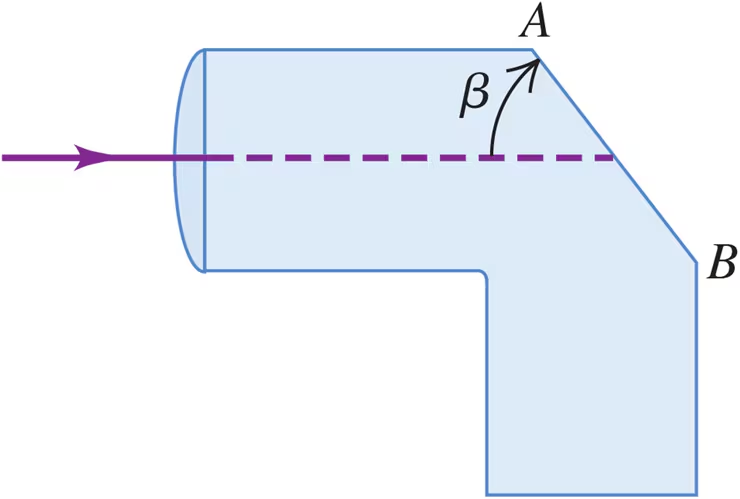
Light enters a solid pipe made of plastic having an index of refraction of 1.60. The light travels parallel to the upper part of the pipe (Fig. E33.15). You want to cut the face AB so that all the light will reflect back into the pipe after it first strikes that face. What is the largest that u can be if the pipe is in air?
Problem 15b
Light enters a solid pipe made of plastic having an index of refraction of 1.60. The light travels parallel to the upper part of the pipe (Fig. E33.15). You want to cut the face AB so that all the light will reflect back into the pipe after it first strikes that face. If the pipe is immersed in water of refractive index 1.33, what is the largest that u can be?
Problem 17a
The critical angle for total internal reflection at a liquid–air interface is 42.5°. If a ray of light traveling in the liquid has an angle of incidence at the interface of 35.0°, what angle does the refracted ray in the air make with the normal?
Problem 20
At the very end of Wagner's series of operas Ring of the Nibelung, Brünnhilde takes the golden ring from the finger of the dead Siegfried and throws it into the Rhine, where it sinks to the bottom of the river. Assuming that the ring is small enough compared to the depth of the river to be treated as a point and that the Rhine is 10.0 m deep where the ring goes in, what is the area of the largest circle at the surface of the water over which light from the ring could escape from the water?
Problem 22
The indexes of refraction for violet light (λ = 400 nm) and red light (λ= 700 nm) in diamond are 2.46 and 2.41, respectively. A ray of light traveling through air strikes the diamond surface at an angle of 53.5° to the normal. Calculate the angular separation between these two colors of light in the refracted ray.
Problem 22b
It is proposed to store 1.00 kWh = 3.60 × 106 J of electrical energy in a uniform magnetic field with magnitude 0.600 T. If instead this amount of energy is to be stored in a volume (in vacuum) equivalent to a cube 40.0 cm on a side, what magnetic field is required?
Problem 24b
A beam of light strikes a sheet of glass at an angle of 57.0° with the normal in air. You observe that red light makes an angle of 38.1° with the normal in the glass, while violet light makes a 36.7° angle. What are the speeds of red and violet light in the glass?
Problem 25
Unpolarized light with intensity I0 is incident on two polarizing filters. The axis of the first filter makes an angle of 60.0° with the vertical, and the axis of the second filter is horizontal. What is the intensity of the light after it has passed through the second filter?
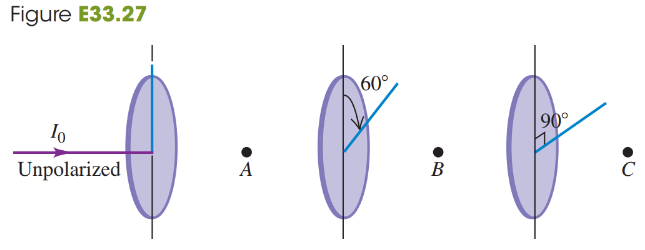
Problem 27b
A beam of unpolarized light of intensity I0 passes through a series of ideal polarizing filters with their polarizing axes turned to various angles as shown in Fig. E33.27. If we remove the middle filter, what will be the light intensity at point C?
Problem 28a
Light of original intensity I0 passes through two ideal polarizing filters having their polarizing axes oriented as shown in Fig. E33.28. You want to adjust the angle f so that the intensity at point P is equal to I0/10. If the original light is unpolarized, what should Φ be?
Problem 28b
Light of original intensity I0 passes through two ideal polarizing filters having their polarizing axes oriented as shown in Fig. E33.28. You want to adjust the angle f so that the intensity at point P is equal to I0/10. If the original light is linearly polarized in the same direction as the polarizing axis of the first polarizer the light reaches, what should Φ be?
Problem 35a
A beam of white light passes through a uniform thickness of air. If the intensity of the scattered light in the middle of the green part of the visible spectrum is I, find the intensity (in terms of I) of scattered light in the middle of the red part of the spectrum.