Back
BackProblem 52b
Equation 20.3 is the mean free path of a particle through a gas of identical particles of equal radius. An electron can be thought of as a point particle with zero radius. Electrons travel 3.0 km through the Stanford Linear Accelerator. In order for scattering losses to be negligible, the pressure inside the accelerator tube must be reduced to the point where the mean free path is at least 50 km. What is the maximum possible pressure inside the accelerator tube, assuming T = 20℃? Give your answer in both Pa and atm.
Problem 53
Uranium has two naturally occurring isotopes. has a natural abundance of and has an abundance of . It is the rarer that is needed for nuclear reactors. The isotopes are separated by forming uranium hexafluoride, , which is a gas, then allowing it to diffuse through a series of porous membranes. has a slightly larger rms speed than and diffuses slightly faster. Many repetitions of this procedure gradually separate the two isotopes. What is the ratio of the rms speed of to that of ?
Problem 54
On earth, STP is based on the average atmospheric pressure at the surface and on a phase change of water that occurs at an easily produced temperature, being only slightly cooler than the average air temperature. The atmosphere of Venus is almost entirely carbon dioxide (CO2), the pressure at the surface is a staggering 93 atm, and the average temperature is 470℃. Venusian scientists, if they existed, would certainly use the surface pressure as part of their definition of STP. To complete the definition, they would seek a phase change that occurs near the average temperature. Conveniently, the melting point of the element tellurium is 450℃. What are (a) the rms speed and (b) the mean free path of carbon dioxide molecules at Venusian STP based on this phase change in tellurium? The radius of a CO2 molecule is 1.5 x 10-10 m.
Problem 55
5.0 x 1023 nitrogen molecules collide with a 10 cm2 wall each second. Assume that the molecules all travel with a speed of 400 m/s and strike the wall head-on. What is the pressure on the wall?
Problem 57
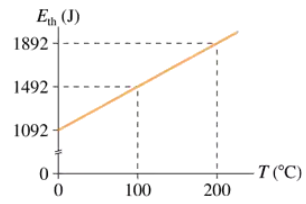
FIGURE P20.57 shows the thermal energy of 0.14 mol of gas as a function of temperature. What is Cᵥ for this gas?
Problem 58b
A 100 cm³ box contains helium at a pressure of 2.0 atm and a temperature of 100℃. It is placed in thermal contact with a 200 cm³ box containing argon at a pressure of 4.0 atm and a temperature of 400℃. What is the final thermal energy of each gas?
Problem 58c
A 100 cm³ box contains helium at a pressure of 2.0 atm and a temperature of 100℃. It is placed in thermal contact with a 200 cm³ box containing argon at a pressure of 4.0 atm and a temperature of 400℃. How much heat energy is transferred, and in which direction?
Problem 59
A gas of 1.0 x 1020 atoms or molecules has 1.0 J of thermal energy. Its molar specific heat at constant pressure is 20.8 J/ mol K. What is the temperature of the gas?
Problem 60c
2.0 g of helium at an initial temperature of 300 K interacts thermally with 8.0 g of oxygen at an initial temperature of 600 K. How much heat energy is transferred, and in which direction?
Problem 61a
What is the total rotational kinetic energy of 1.0 mol of nitrogen gas at 300 K?
Problem 61b
A nitrogen molecule consists of two nitrogen atoms separated by 0.11 nm, the bond length. Treat the molecule as a rotating dumbbell and find the rms angular velocity at this temperature of a nitrogen molecule around the z-axis, as shown in Figure 20.10.
Problem 63
A water molecule has its three atoms arranged in a 'V' shape, so it has rotational kinetic energy around any of three mutually perpendicular axes. However, like diatomic molecules, its vibrational modes are not active at temperatures below 1000 K. What is the thermal energy of 2.0 mol of steam at a temperature of 160°C?
Problem 65b
A monatomic gas is adiabatically compressed to 1/8 of its initial volume. Does each of the following quantities change? If so, does it increase or decrease, and by what factor? If not, why not? The mean free path.
Problem 65c
A monatomic gas is adiabatically compressed to 1/8 of its initial volume. Does each of the following quantities change? If so, does it increase or decrease, and by what factor? If not, why not? The thermal energy of the gas.
Problem 66b
n moles of a diatomic gas with Cv = 5/2 R has initial pressure pi and volume Vi. The gas undergoes a process in which the pressure is directly proportional to the volume until the rms speed of the molecules has doubled. How much heat does this process require? Give your answer in terms of n, pi and Vi.
Problem 67
The 2010 Nobel Prize in Physics was awarded for the discovery of graphene, a two-dimensional form of carbon in which the atoms form a two-dimensional crystal-lattice sheet only one atom thick. Predict the molar specific heat of graphene. Give your answer as a multiple of R.
Problem 68c
The rms speed of the molecules in 1.0 g of hydrogen gas is 1800 m/s. 500 J of work are done to compress the gas while, in the same process, 1200 J of heat energy are transferred from the gas to the environment. Afterward, what is the rms speed of the molecules?
Problem 69a
n1 moles of a monatomic gas and n2 moles of a diatomic gas are mixed together in a container. Derive an expression for the molar specific heat at constant volume of the mixture.
Problem 71
A thin partition divides a container of volume V into two parts. One side contains nA moles of gas A in a fraction fA of the container; that is, VA = fAV. The other side contains nB moles of a different gas B at the same temperature in a fraction fB of the container. The partition is removed, allowing the gases to mix. Find an expression for the change of entropy. This is called the entropy of mixing.
Problem 72
An experiment you're designing needs a gas with γ = 1.50. You recall from your physics class that no individual gas has this value, but it occurs to you that you could produce a gas with γ = 1.50 by mixing together a monatomic gas and a diatomic gas. What fraction of the molecules need to be monatomic?
Problem 73a
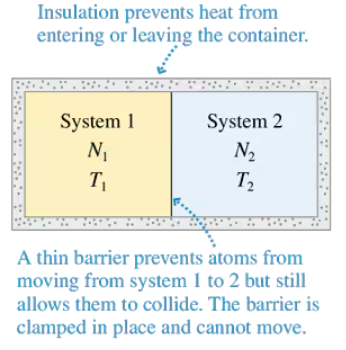
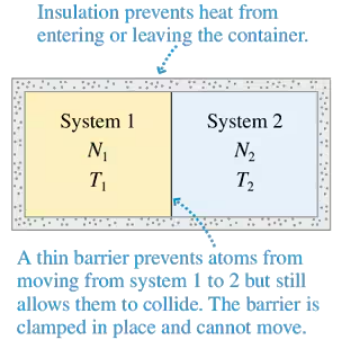
Consider a container like that shown in Figure, with moles of a monatomic gas on one side and moles of a diatomic gas on the other. The monatomic gas has initial temperature . The diatomic gas has initial temperature . Show that the equilibrium thermal energies are
Problem 73b
Consider a container like that shown in the Figure, with moles of a monatomic gas on one side and moles of a diatomic gas on the other. The monatomic gas has initial temperature . The diatomic gas has initial temperature . Show that the equilibrium temperature is
Problem 75
A 2.0 mol sample of oxygen gas in a rigid, 15 L container is slowly cooled from 250℃ to 50℃ by being in thermal contact with a large bath of 50℃ water. What is the entropy change of (a) the gas and (b) the universe?