When the displacement of a mass on a spring is (½)A, what fraction of the energy is kinetic energy and what fraction is potential energy?

A 100 g block attached to a spring with spring constant 2.5 N/m oscillates horizontally on a frictionless table. Its velocity is 20 c/m when 𝓍 = -5.0 cm What is the block's position when the acceleration is maximum?

An ultrasonic transducer, of the type used in medical ultrasound imaging, is a very thin disk (m = 0.10 g) driven back and forth in SHM at 1.0 MHz by an electromagnetic coil. What is the disk's maximum speed at this amplitude?

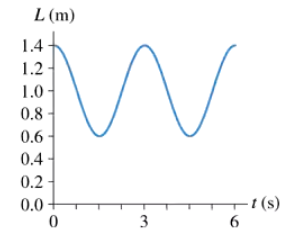
Astronauts in space cannot weigh themselves by standing on a bathroom scale. Instead, they determine their mass by oscillating on a large spring. Suppose an astronaut attaches one end of a large spring to her belt and the other end to a hook on the wall of the space capsule. A fellow astronaut then pulls her away from the wall and releases her. The spring's length as a function of time is shown in FIGURE P15.46. What is her speed when the spring's length is 1.2 m?

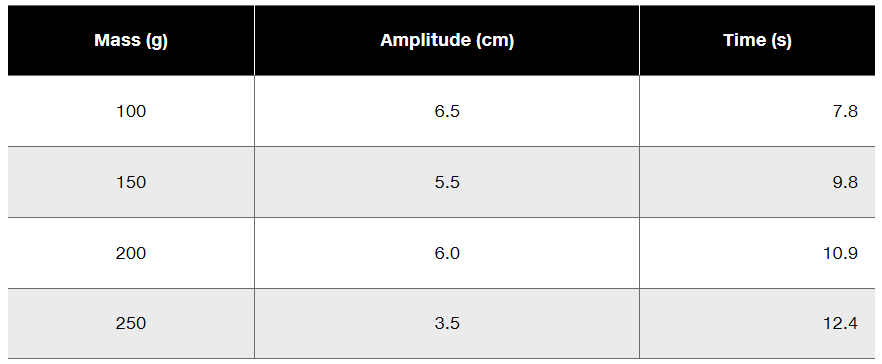
Your lab instructor has asked you to measure a spring constant using a dynamic method—letting it oscillate—rather than a static method of stretching it. You and your lab partner suspend the spring from a hook, hang different masses on the lower end, and start them oscillating. One of you uses a meter stick to measure the amplitude, the other uses a stopwatch to time 10 oscillations. Your data are as follows: Use the best-fit line of an appropriate graph to determine the spring constant.

A 200 g block hangs from a spring with spring constant 10 N/m. At t = 0 s the block is 20 cm below the equilibrium point and moving upward with a speed of 100 cm/s. What are the block's a. Oscillation frequency?

A 200 g block hangs from a spring with spring constant 10 N/m. At t = 0 s the block is 20 cm below the equilibrium point and moving upward with a speed of 100 cm/s. What are the block's distance from equilibrium when the speed is 50 cm/s?

A 500 g wood block on a frictionless table is attached to a horizontal spring. A 50 g dart is shot into the face of the block opposite the spring, where it sticks. Afterward, the spring oscillates with a period of 1.5 s and an amplitude of 20 cm. How fast was the dart moving when it hit the block?

Scientists are measuring the properties of a newly discovered elastic material. They create a 1.5-m-long, 1.6-mm-diameter cord, attach an 850 g mass to the lower end, then pull the mass down 2.5 mm and release it. Their high-speed video camera records 36 oscillations in 2.0 s. What is Young's modulus of the material?

A mass hanging from a spring oscillates with a period of 0.35 s. Suppose the mass and spring are swung in a horizontal circle, with the free end of the spring at the pivot. What rotation frequency, in rpm, will cause the spring's length to stretch by 15%?

A compact car has a mass of 1200 kg. Assume that the car has one spring on each wheel, that the springs are identical, and that the mass is equally distributed over the four springs. What will be the car's oscillation frequency while carrying four 70 kg passengers?

A 1.00 kg block is attached to a horizontal spring with spring constant 2500 N/m. The block is at rest on a frictionless surface. A 10 g bullet is fired into the block, in the face opposite the spring, and sticks. What was the bullet's speed if the subsequent oscillations have an amplitude of 10.0 cm?

Interestingly, there have been several studies using cadavers to determine the moments of inertia of human body parts, information that is important in biomechanics. In one study, the center of mass of a 5.0 kg lower leg was found to be 18 cm from the knee. When the leg was allowed to pivot at the knee and swing freely as a pendulum, the oscillation frequency was 1.6 Hz. What was the moment of inertia of the lower leg about the knee joint?

It has recently become possible to 'weigh' DNA molecules by measuring the influence of their mass on a nano-oscillator. FIGURE P15.58 shows a thin rectangular cantilever etched out of silicon (density 2300 kg/m³) with a small gold dot (not visible) at the end. If pulled down and released, the end of the cantilever vibrates with SHM, moving up and down like a diving board after a jump. When bathed with DNA molecules whose ends have been modified to bind with gold, one or more molecules may attach to the gold dot. The addition of their mass causes a very slight—but measurable—decrease in the oscillation frequency. A vibrating cantilever of mass M can be modeled as a block of mass ⅓M attached to a spring. (The factor of ⅓ arises from the moment of inertia of a bar pivoted at one end.) Neither the mass nor the spring constant can be determined very accurately—perhaps to only two significant figures—but the oscillation frequency can be measured with very high precision simply by counting the oscillations. In one experiment, the cantilever was initially vibrating at exactly 12 MHz. Attachment of a DNA molecule caused the frequency to decrease by 50 Hz. What was the mass of the DNA?

A uniform rod of mass M and length L swings as a pendulum on a pivot at distance L/4 from one end of the rod. Find an expression for the frequency f of small-angle oscillations.

A 500 g air-track glider attached to a spring with spring constant 10 N/m is sitting at rest on a frictionless air track. A 250 g glider is pushed toward it from the far end of the track at a speed of 120 cm/s. It collides with and sticks to the 500 g glider. What are the amplitude and period of the subsequent oscillations?

A 15-cm-long, 200 g rod is pivoted at one end. A 20 g ball of clay is stuck on the other end. What is the period if the rod and clay swing as a pendulum?

The 15 g head of a bobble-head doll oscillates in SHM at a frequency of 4.0 Hz. The amplitude of the head's oscillations decreases to 0.5 cm in 4.0 s. What is the head's damping constant?

A 200 g oscillator in a vacuum chamber has a frequency of 2.0 Hz. When air is admitted, the oscillation decreases to 60% of its initial amplitude in 50 s. How many oscillations will have been completed when the amplitude is 30% of its initial value?

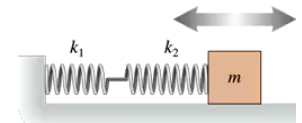
A block on a frictionless table is connected as shown in FIGURE P15.75 to two springs having spring constants k₁ and k₂. Find an expression for the block’s oscillation frequency f in terms of the frequencies f₁ and f₂ at which it would oscillate if attached to spring 1 or spring 2 alone.

Suppose a large spherical object, such as a planet, with radius R and mass M has a narrow tunnel passing diametrically through it. A particle of mass m is inside the tunnel at a distance 𝓍 ≤ R from the center. It can be shown that the net gravitational force on the particle is due entirely to the sphere of mass with radius 𝓇 ≤ 𝓍 there is no net gravitational force from the mass in the spherical shell with 𝓇 > 𝓍. a. Find an expression for the gravitational force on the particle, assuming the object has uniform density. Your expression will be in terms of x, R, m, M, and any necessary constants.

A uniform rod of length L oscillates as a pendulum about a pivot that is a distance x from the center. For what value of x, in terms of L, is the oscillation period a minimum?

A spring is standing upright on a table with its bottom end fastened to the table. A block is dropped from a height 3.0 cm above the top of the spring. The block sticks to the top end of the spring and then oscillates with an amplitude of 10 cm. What is the oscillation frequency?

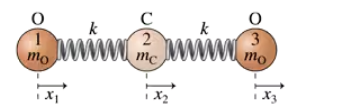
The greenhouse-gas carbon dioxide molecule CO₂ strongly absorbs infrared radiation when its vibrational normal modes are excited by light at the normal-mode frequencies. CO₂ is a linear triatomic molecule, as shown in FIGURE CP15.82, with oxygen atoms of mass mo bonded to a central carbon atom of mass m_c. You know from chemistry that the atomic masses of carbon and oxygen are, respectively, 12 and 16. Assume that the bond is an ideal spring with spring constant k. There are two normal modes of this system for which oscillations take place along the axis. (You can ignore additional bending modes.) In this problem, you will find the normal modes and then use experimental data to determine the bond spring constant. The symmetric stretch frequency is known to be 4.00 X 10¹³ Hz. What is the spring constant of the C - O bond? Use 1 u = 1 atomic mass unit = 1.66 X 10⁻²⁷ kg to find the atomic masses in SI units. Interestingly, the spring constant is similar to that of springs you might use in the lab.

The greenhouse-gas carbon dioxide molecule CO₂ strongly absorbs infrared radiation when its vibrational normal modes are excited by light at the normal-mode frequencies. CO₂ is a linear triatomic molecule, as shown in FIGURE CP15.82, with oxygen atoms of mass mo bonded to a central carbon atom of mass m_c. You know from chemistry that the atomic masses of carbon and oxygen are, respectively, 12 and 16. Assume that the bond is an ideal spring with spring constant k. There are two normal modes of this system for which oscillations take place along the axis. (You can ignore additional bending modes.) In this problem, you will find the normal modes and then use experimental data to determine the bond spring constant. Use the frequency of the symmetric stretch to predict the frequency of the antisymmetric stretch. The measured frequency is 7.05 × 10¹³ Hz so your prediction is close but not perfect. The reason is that the bonds are not ideal springs but have a slight amount of anharmonicity. Nonetheless, you’ve learned a great deal about the CO₂ molecule from a simple model of oscillating masses.