Back
BackProblem 60
Water from a vertical pipe emerges as a 10-cm-diameter cylinder and falls straight down 7.5 m into a bucket. The water exits the pipe with a speed of 2.0 m/s. What is the diameter of the column of water as it hits the bucket?
Problem 61b
A hurricane wind blows across a 6.0 m x 15.0 m flat roof at a speed of 130 km/h. What is the pressure difference?
Problem 62
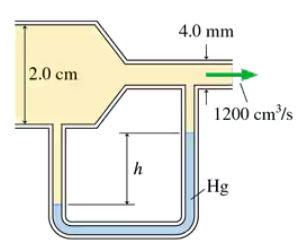
Air flows through the tube shown in FIGURE P14.62 at a rate of 1200 cm³/s. Assume that air is an ideal fluid. What is the height h of mercury in the right side of the U-tube?
Problem 63b
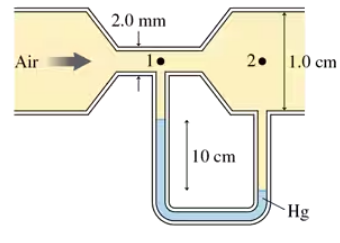
Air flows through the tube shown in FIGURE P14.63. Assume that air is an ideal fluid. What is the volume flow rate?
Problem 64a
A water tank of height h has a small hole at height y. The water is replenished to keep h from changing. The water squirting from the hole has range 𝓍. The range approaches zero as y → 0 because the water squirts right onto the ground. The range also approaches zero as y → h because the horizontal velocity becomes zero. Thus there must be some height y between 0 and h for which the range is a maximum. Find an algebraic expression for the flow speed v with which the water exits the hole at height y.
Problem 65a
A cylindrical tank of radius 𝑅, filled to the top with a liquid, has a small hole in the side, of radius 𝓇, at distance d below the surface. Find an expression for the volume flow rate through the hole.
Problem 66
20°C water flows through a 2.0-m-long, 6.0-mm-diameter pipe. What is the maximum flow rate in L/min for which the flow is laminar?
Problem 67
20°C water flows at 1.5 m/s through a 10-m-long, 1.0-mm-diameter horizontal tube and then exits into the air. What is the gauge pressure in kPa at the point where the water enters the tube?
Problem 68
The 30-cm-long left coronary artery is 4.6 mm in diameter. Blood pressure drops by 3.0 mm of mercury over this distance. What are the (a) average blood speed and (b) volume flow rate in L/min through this artery?
Problem 71
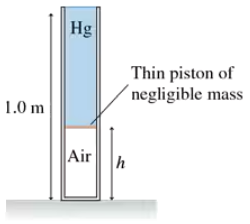
The 1.0-m-tall cylinder shown in FIGURE CP14.71 contains air at a pressure of 1 atm. A very thin, frictionless piston of negligible mass is placed at the top of the cylinder to prevent any air from escaping, then mercury is slowly poured into the cylinder until no more can be added without the cylinder overflowing. What is the height h of the column of compressed air? Hint: Boyle's law, which you learned in chemistry, says p₁V₁ = p₂V₂ for a gas compressed at constant temperature, which we will assume to be the case.
Problem 72
The bottom of a steel 'boat' is a 5.0 m x 10 m x 2.0 cm piece of steel (psteel = 7900 kg/m³). The sides are made of 0.50-cm-thick steel. What minimum height must the sides have for this boat to float in perfectly calm water?
Problem 73a
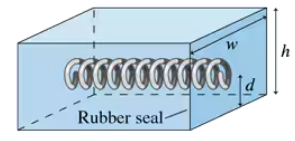
The tank shown in FIGURE CP14.73 is completely filled with a liquid of density ρ. The right face is not permanently attached to the tank but, instead, is held against a rubber seal by the tension in a spring. To prevent leakage, the spring must both pull with sufficient strength and prevent a torque from pushing the bottom of the right face out. What minimum spring tension is needed?
Problem 73b
The tank shown in FIGURE CP14.73 is completely filled with a liquid of density ρ. The right face is not permanently attached to the tank but, instead, is held against a rubber seal by the tension in a spring. To prevent leakage, the spring must both pull with sufficient strength and prevent a torque from pushing the bottom of the right face out. If the spring has the minimum tension, at what height d from the bottom must it be attached?
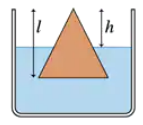
Problem 74
In FIGURE CP14.74, a cone of density ρ0 and total height l floats in a liquid of density ρf. The height of the cone above the liquid is h. What is the ratio h/l of the exposed height to the total height?