The two stars in a binary star system have masses 2.0 x 10³⁰ kg and 6.0 x 10³⁰ kg. They are separated by 2.0 x 10¹² m. What are The speed of each star?

A starship is circling a distant planet of radius R. The astronauts find that the free-fall acceleration at their altitude is half the value at the planet's surface. How far above the surface are they orbiting? Your answer will be a multiple of R.

A 4000 kg lunar lander is in orbit 50 km above the surface of the moon. It needs to move out to a 300-km-high orbit in order to link up with the mother ship that will take the astronauts home. How much work must the thrusters do?

The 75,000 kg space shuttle used to fly in a 250-km-high circular orbit. It needed to reach a 610-km-high circular orbit to service the Hubble Space Telescope. How much energy was required to boost it to the new orbit?

In 2000, NASA placed a satellite in orbit around an asteroid. Consider a spherical asteroid with a mass of 1.0 x 10¹⁶ kg and a radius of 8.8 km. What is the escape speed from the asteroid?

In 2014, the European Space Agency placed a satellite in orbit around comet 67P/Churyumov-Gerasimenko and then landed a probe on the surface. The actual orbit was elliptical, but we’ll approximate it as a 50-km-diameter circular orbit with a period of 11 days. What is the mass of the comet?

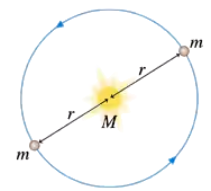
FIGURE P13.57 shows two planets of mass m orbiting a star of mass M. The planets are in the same orbit, with radius r, but are always at opposite ends of a diameter. Find an exact expression for the orbital period T. Hint: Each planet feels two forces.

Large stars can explode as they finish burning their nuclear fuel, causing a supernova. The explosion blows away the outer layers of the star. According to Newton’s third law, the forces that push the outer layers away have reaction forces that are inwardly directed on the core of the star. These forces compress the core and can cause the core to undergo a gravitational collapse. The gravitational forces keep pulling all the matter together tighter and tighter, crushing atoms out of existence. Under these extreme conditions, a proton and an electron can be squeezed together to form a neutron. If the collapse is halted when the neutrons all come into contact with each other, the result is an object called a neutron star, an entire star consisting of solid nuclear matter. Many neutron stars rotate about their axis with a period of ≈ 1 s and, as they do so, send out a pulse of electromagnetic waves once a second. These stars were discovered in the 1960s and are called pulsars. How many revolutions per minute are made by a satellite orbiting 1.0 km above the surface?

Large stars can explode as they finish burning their nuclear fuel, causing a supernova. The explosion blows away the outer layers of the star. According to Newton's third law, the forces that push the outer layers away have reaction forces that are inwardly directed on the core of the star. These forces compress the core and can cause the core to undergo a gravitational collapse. The gravitational forces keep pulling all the matter together tighter and tighter, crushing atoms out of existence. Under these extreme conditions, a proton and an electron can be squeezed together to form a neutron. If the collapse is halted when the neutrons all come into contact with each other, the result is an object called a neutron star, an entire star consisting of solid nuclear matter. Many neutron stars rotate about their axis with a period of ≈ 1 s and, as they do so, send out a pulse of electromagnetic waves once a second. These stars were discovered in the 1960s and are called pulsars. What is the radius of a geosynchronous orbit?

The solar system is 25,000 light years from the center of our Milky Way galaxy. One light year is the distance light travels in one year at a speed of 3.0 x 10⁶ m/s . Astronomers have determined that the solar system is orbiting the center of the galaxy at a speed of 230 km/s . Our solar system was formed roughly 5 billion years ago. How many orbits has it completed?

The solar system is 25,000 light years from the center of our Milky Way galaxy. One light year is the distance light travels in one year at a speed of 3.0 x 10⁸ m/s. Astronomers have determined that the solar system is orbiting the center of the galaxy at a speed of 230 km/s. The gravitational force on the solar system is the net force due to all the matter inside our orbit. Most of that matter is concentrated near the center of the galaxy. Assume that the matter has a spherical distribution, like a giant star. What is the approximate mass of the galactic center?

The solar system is 25,000 light years from the center of our Milky Way galaxy. One light year is the distance light travels in one year at a speed of 3.0 x 10⁸ m/s. Astronomers have determined that the solar system is orbiting the center of the galaxy at a speed of 230 km/s. Assume that the sun is a typical star with a typical mass. If galactic matter is made up of stars, approximately how many stars are in the center of the galaxy?

Three stars, each with the mass of our sun, form an equilateral triangle with sides 1.0 x 10¹² m long. (This triangle would just about fit within the orbit of Jupiter.) The triangle has to rotate, because otherwise the stars would crash together in the center. What is the period of rotation?

Comets move around the sun in very elliptical orbits. At its closet approach, in 1986, Comet Halley was 8.79 x 10⁷ km from the sun and moving with a speed of 54.6 km/s. What was the comet’s speed when it crossed Neptune’s orbit in 2006?

A 55,000 kg space capsule is in a 28,000-km-diameter circular orbit around the moon. A brief but intense firing of its engine in the forward direction suddenly decreases its speed by 50%. This causes the space capsule to go into an elliptical orbit. What are the space capsule’s (a) maximum and (b) minimum distances from the center of the moon in its new orbit? Hint: You will need to use two conservation laws.

Two Jupiter-size planets are released from rest 1.0 x 10¹¹ m apart. What are their speeds as they crash together?

A satellite in a circular orbit of radius r has period T. A satellite in a nearby orbit with radius r + Δr, where Δr ≪ r, has the very slightly different period T + ΔT. Show that ΔT/T = (3/2) (Δr/r)

While visiting Planet Physics, you toss a rock straight up at 11 m/s and catch it 2.5 s later. While you visit the surface, your cruise ship orbits at an altitude equal to the planet's radius every 230 min. What are the (a) mass and (b) radius of Planet Physics?

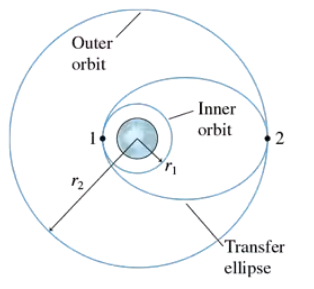
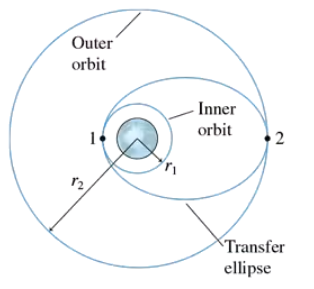
Let’s look in more detail at how a satellite is moved from one circular orbit to another. FIGURE CP13.70 shows two circular orbits, of radii r₁ and r₂, and an elliptical orbit that connects them. Points 1 and 2 are at the ends of the semimajor axis of the ellipse. Consider a 1000 kg communications satellite that needs to be boosted from an orbit 300 km above the earth to a geosynchronous orbit 35,900 km above the earth. Find the velocity v'₁ on the inner circular orbit and the velocity v'₁ at the low point on the elliptical orbit that spans the two circular orbits.

Let's look in more detail at how a satellite is moved from one circular orbit to another. FIGURE CP13.70 shows two circular orbits, of radii r₁ and r₂, and an elliptical orbit that connects them. Points 1 and 2 are at the ends of the semimajor axis of the ellipse. How much work must the rocket motor do to transfer the satellite from the circular orbit to the elliptical orbit?

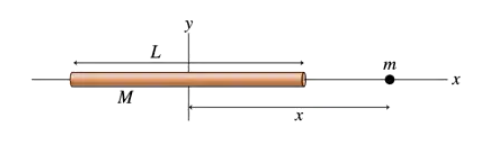
FIGURE CP13.71 shows a particle of mass m at distance 𝓍 from the center of a very thin cylinder of mass M and length L. The particle is outside the cylinder, so 𝓍 > L/2 . Calculate the gravitational potential energy of these two masses.

September 2015 saw the historic discovery of gravitational waves, almost exactly 100 years after Einstein predicted their existence as a consequence of his theory of general relativity. Gravitational waves are a literal stretching and compressing of the fabric of space. Even the most sensitive instruments—capable of sensing that the path of a 4-km-long laser beam has lengthened by one-thousandth the diameter of a proton—can detect waves created by only the most extreme cosmic events. The first detection was due to the collision of two black holes more than 750 million light years from earth. Although a full description of gravitational waves requires knowledge of Einstein's general relativity, a surprising amount can be understood with the physics you've already learned. Two black holes collide and merge when their Schwarzchild radii overlap; that is, they merge when their separation, which we've defined as 2r, equals 2R_Sch . Find an expression for ΔE=E_f−E_i , where E_i ≈ 0 because initially the black holes are far apart and E_f is their total energy at the instant they merge. This is the energy radiated away as gravitational waves. Your answer will be a fraction of Mc², and you probably recognize that this is related to Einstein's famous E=mc² . The quantity Mc² is the amount of energy that would be released if an entire star of mass M were suddenly converted entirely to energy.