Back
BackProblem 77a
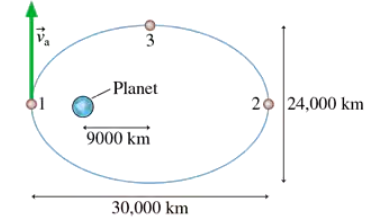
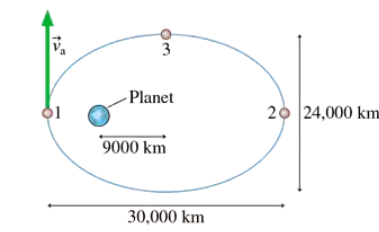
A satellite follows the elliptical orbit shown in FIGURE P12.77. The only force on the satellite is the gravitational attraction of the planet. The satellite's speed at point 1 is 8000 m/s. Does the satellite experience any torque about the center of the planet? Explain.
Problem 77b
A satellite follows the elliptical orbit shown in FIGURE P12.77. The only force on the satellite is the gravitational attraction of the planet. The satellite's speed at point 1 is 8000 m/s. What is the satellite's speed at point 2?
Problem 78
A 10 g bullet traveling at 400 m/s strikes a 10 kg, 1.0-m-wide door at the edge opposite the hinge. The bullet embeds itself in the door, causing the door to swing open. What is the angular velocity of the door just after impact?
Problem 81
A merry-go-round is a common piece of playground equipment. A 3.0-m-diameter merry-go-round with a mass of 250 kg is spinning at 20 rpm. John runs tangent to the merry-go-round at 5.0 m/s, in the same direction that it is turning, and jumps onto the outer edge. John's mass is 30 kg. What is the merry-go-round's angular velocity, in rpm, after John jumps on?
Problem 82
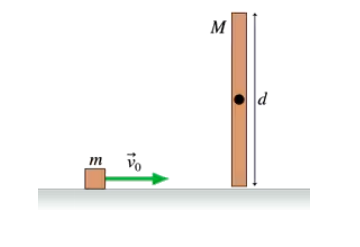
FIGURE P12.82 shows a cube of mass m sliding without friction at speed v0. It undergoes a perfectly elastic collision with the bottom tip of a rod of length d and mass M = 2m. The rod is pivoted about a frictionless axle through its center, and initially it hangs straight down and is at rest. What is the cube's velocity—both speed and direction—after the collision?
Problem 83a
During most of its lifetime, a star maintains an equilibrium size in which the inward force of gravity on each atom is balanced by an outward pressure force due to the heat of the nuclear reactions in the core. But after all the hydrogen 'fuel' is consumed by nuclear fusion, the pressure force drops and the star undergoes a gravitational collapse until it becomes a neutron star. In a neutron star, the electrons and protons of the atoms are squeezed together by gravity until they fuse into neutrons. Neutron stars spin very rapidly and emit intense pulses of radio and light waves, one pulse per rotation. These 'pulsing stars' were discovered in the 1960s and are called pulsars. a. A star with the mass (M = 2.0 X 1030 kg) and size (R = 7.0 x 108 m) of our sun rotates once every 30 days. After undergoing gravitational collapse, the star forms a pulsar that is observed by astronomers to emit radio pulses every 0.10 s. By treating the neutron star as a solid sphere, deduce its radius.
Problem 85
Objects that rotate in air or water experience a torque due to drag. With quadratic drag, a drag torque that's negligible at low rpm quickly becomes significant as the rpm increases. Consider a square bar with cross section a x a and length L. It is rotating on an axle through its center at angular velocity ω in a fluid of density ρ. Assume that the drag coefficient C𝒹 is constant along the length of the bar. Find an expression for the magnitude of the drag torque on the bar. Hint: Begin by considering the drag force on a small piece of the bar of length dr at distance r from the axle.
Problem 86
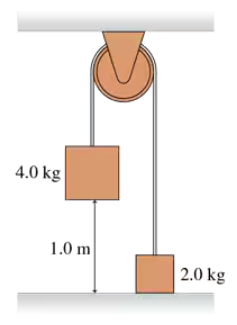
The two blocks in FIGURE CP12.86 are connected by a massless rope that passes over a pulley. The pulley is 12 cm in diameter and has a mass of 2.0 kg. As the pulley turns, friction at the axle exerts a torque of magnitude 0.50 N m. If the blocks are released from rest, how long does it take the 4.0 kg block to reach the floor?
Problem 88b
A rod of length L and mass M has a nonuniform mass distribution. The linear mass density (mass per length) is λ = cx2, where x is measured from the center of the rod and c is a constant. Find an expression for c in terms of L and M.
Problem 88c
A rod of length L and mass M has a nonuniform mass distribution. The linear mass density (mass per length) is λ = cx2 , where x is measured from the center of the rod and c is a constant. Find an expression in terms of L and M for the moment of inertia of the rod for rotation about an axis through the center.
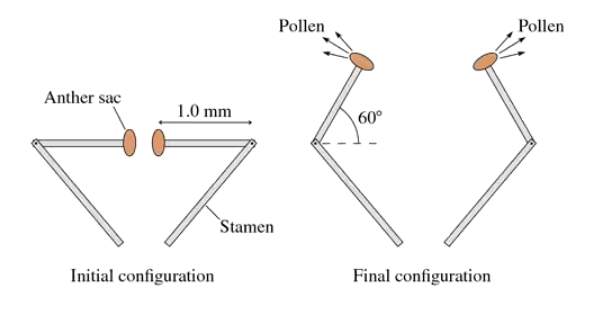
Problem 91b
The bunchberry flower has the fastest-moving parts ever observed in a plant. Initially, the stamens are held by the petals in a bent position, storing elastic energy like a coiled spring. When the petals release, the tips of the stamen act like medieval catapults, flipping through a 60° angle in just 0.30 ms to launch pollen from anther sacs at their ends. The human eye just sees a burst of pollen; only high-speed photography reveals the details. As FIGURE CP12.91 shows, we can model the stamen tip as a 1.0-mm-long, 10 μg rigid rod with a 10 μg anther sac at the end. Although oversimplifying, we'll assume a constant angular acceleration. What is the speed of the anther sac as it releases its pollen?