Vector A ＝ 3î＋ĵ and vector B＝ 3î - 2ĵ ＋ 2k. What is the cross product A ✕ B?

Force $\vec{F}=-10\hat{j}\text{N}$ is exerted on a particle at $\vec{r} = (5\hat{i} + 5\hat{j}) \, \text{m}$. What is the torque on the particle about the origin?

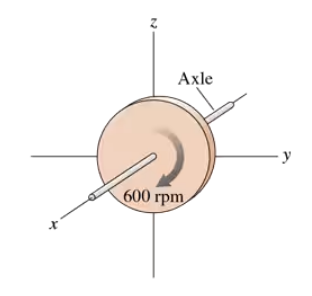
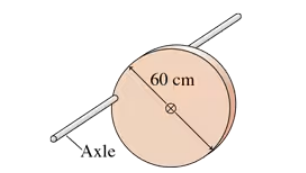
What is the angular momentum vector of the 2.0 kg, 4.0-cm-diameter rotating disk in FIGURE EX12.43? Give your answer using unit vectors.

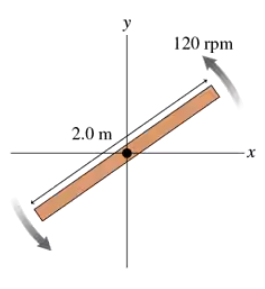
What is the angular momentum vector of the 500 g rotating bar in FIGURE EX12.44? Give your answer using unit vectors.

A 2.0 kg, 20-cm-diameter turntable rotates at 100 rpm on frictionless bearings. Two 500 g blocks fall from above, hit the turntable simultaneously at opposite ends of a diameter, and stick. What is the turntable's angular velocity, in rpm, just after this event?

A 75 g, 6.0-cm-diameter solid spherical top is spun at 1200 rpm on an axle that extends 1.0 cm past the edge of the sphere. The tip of the axle is placed on a support. What is the top's precession frequency in rpm?

A toy gyroscope has a ring of mass M and radius R attached to the axle by lightweight spokes. The end of the axle is distance R from the center of the ring. The gyroscope is spun at angular velocity ω, then the end of the axle is placed on a support that allows the gyroscope to precess. A 120 g, 8.0-cm-diameter gyroscope is spun at 1000 rpm and allowed to precess. What is the precession period?

A small 300 g ball and a small 600 g ball are connected by a 40-cm-long, 200 g rigid rod. a. How far is the center of mass from the 600 g ball?

A small 300 g ball and a small 600 g ball are connected by a 40-cm-long, 200 g rigid rod. b. What is the rotational kinetic energy if the structure rotates about its center of mass at 100 rpm?

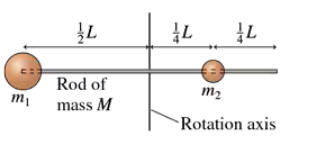
Determine the moment of inertia about the axis of the object shown in FIGURE P12.52.

Calculate by direct integration the moment of inertia for a thin rod of mass M and length L about an axis located distance d from one end. Confirm that your answer agrees with Table 12.2 when d=0 and when d = L/2.

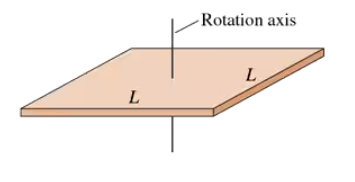
Calculate the moment of inertia of the rectangular plate in FIGURE P12.55 for rotation about a perpendicular axis through the center.

A 4.0-cm-diameter disk with a 3.0-cm-diameter hole rolls down a 50-cm-long, 20° ramp. What is its speed at the bottom? What percent is this of the speed of a particle sliding down a frictionless ramp?

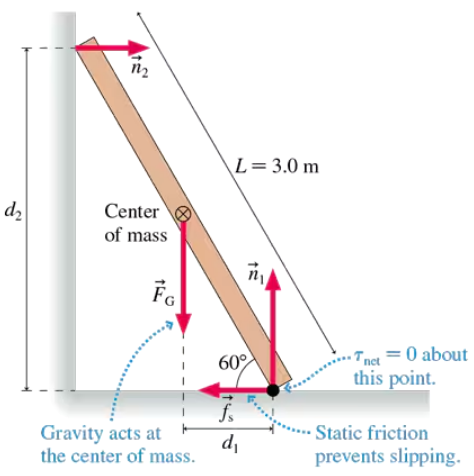
A 3.0-m-long ladder, as shown in Figure 12.35, leans against a frictionless wall. The coefficient of static friction between the ladder and the floor is 0.40. What is the minimum angle the ladder can make with the floor without slipping?

A person's center of mass is easily found by having the person lie on a reaction board. A horizontal, 2.5-m-long, 6.1 kg reaction board is supported only at the ends, with one end resting on a scale and the other on a pivot. A 60 kg woman lies on the reaction board with her feet over the pivot. The scale reads 25 kg. What is the distance from the woman's feet to her center of mass?

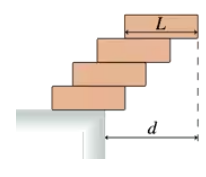
Your task in a science contest is to stack four identical uniform bricks, each of length L, so that the top brick is as far to the right as possible without the stack falling over. Is it possible, as FIGURE P12.60 shows, to stack the bricks such that no part of the top brick is over the table? Answer this question by determining the maximum possible value of d.

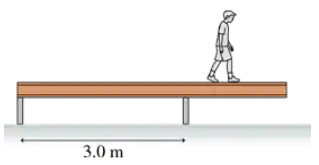
A 40 kg, 5.0-m-long beam is supported by, but not attached to, the two posts in FIGURE P12.61. A 20 kg boy starts walking along the beam. How close can he get to the right end of the beam without it falling over?

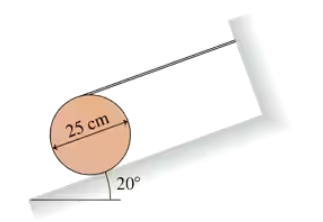
FIGURE P12.63 shows a 15 kg cylinder held at rest on a 20° slope. What is the magnitude of the static friction force?

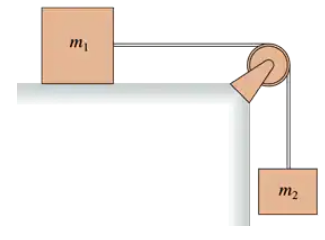
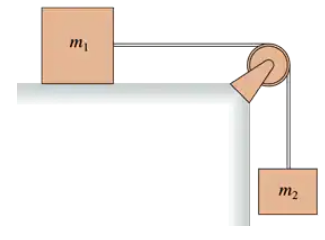
Blocks of mass m₁ and m₂ are connected by a massless string that passes over the pulley in FIGURE P12.64. The pulley turns on frictionless bearings. Mass m₁ slides on a horizontal, frictionless surface. Mass m₂ is released while the blocks are at rest. Assume the pulley is massless. Find the acceleration of m₁ and the tension in the string. This is a Chapter 7 review problem.

Blocks of mass m₁ and m₂ are connected by a massless string that passes over the pulley in FIGURE P12.64. The pulley turns on frictionless bearings. Mass m₁ slides on a horizontal, frictionless surface. Mass m₂ is released while the blocks are at rest. Suppose the pulley has mass m_p and radius R. Find the acceleration of m₁ and the tensions in the upper and lower portions of the string. Verify that your answers agree with part a if you set m_p = 0.

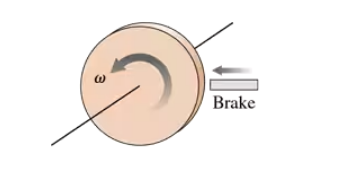
The 2.0 kg, 30-cm-diameter disk in FIGURE P12.65 is spinning at 300 rpm. How much friction force must the brake apply to the rim to bring the disk to a halt in 3.0 s?

Flywheels are large, massive wheels used to store energy. They can be spun up slowly, then the wheel's energy can be released quickly to accomplish a task that demands high power. An industrial flywheel has a 1.5 m diameter and a mass of 250 kg. Its maximum angular velocity is 1200 rpm. How much energy is stored in the flywheel?

A 30-cm-diameter, 1.2 kg solid turntable rotates on a 1.2-cm-diameter, 450 g shaft at a constant 33 rpm. When you hit the stop switch, a brake pad presses against the shaft and brings the turntable to a halt in 15 seconds. How much friction force does the brake pad apply to the shaft?

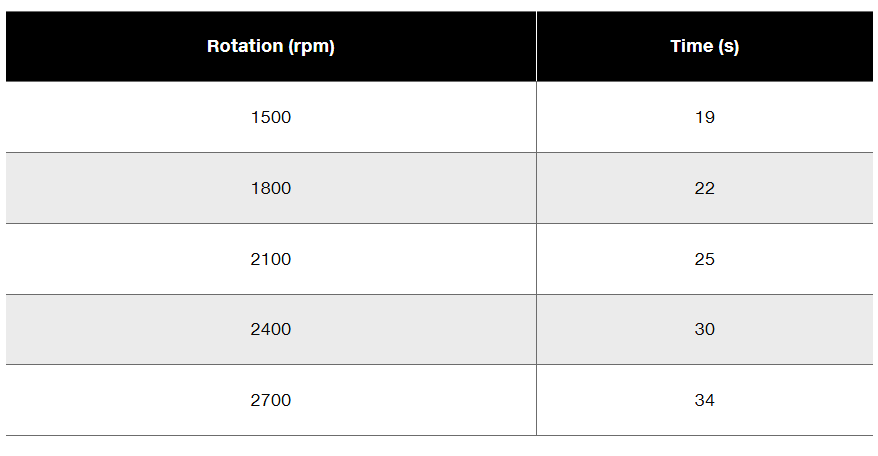
Your engineering team has been assigned the task of measuring the properties of a new jet-engine turbine. You've previously determined that the turbine's moment of inertia is 2.6 kg m². The next job is to measure the frictional torque of the bearings. Your plan is to run the turbine up to a predetermined rotation speed, cut the power, and time how long it takes the turbine to reduce its rotation speed by 50%. Your data are given in the table. Draw an appropriate graph of the data and, from the slope of the best-fit line, determine the frictional torque.

A 750 g disk and a 760 g ring, both 15 cm in diameter, are rolling along a horizontal surface at 1.5 m/s when they encounter a 15° slope. How far up the slope does each travel before rolling back down?

The 5.0 kg, 60-cm-diameter disk in FIGURE P12.71 rotates on an axle passing through one edge. The axle is parallel to the floor. The cylinder is held with the center of mass at the same height as the axle, then released. What is the cylinder's angular velocity when it is directly below the axle?

A solid spherical marble shot up a frictionless 15° slope rolls 2.50 m to its highest point. If the marble is shot with the same speed up a slightly rough 15° slope, it rolls only 2.30 m. What is the coefficient of rolling friction on the second slope?

A long, thin rod of mass M and length L is standing straight up on a table. Its lower end rotates on a frictionless pivot. A very slight push causes the rod to fall over. As it hits the table, what are the angular velocity

A long, thin rod of mass M and length L is standing straight up on a table. Its lower end rotates on a frictionless pivot. A very slight push causes the rod to fall over. As it hits the table, what are the speed of the tip of the rod?

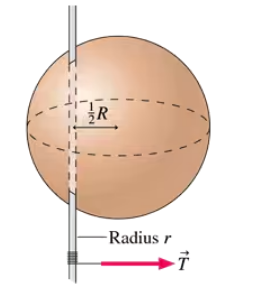
The sphere of mass M and radius R in FIGURE P12.75 is rigidly attached to a thin rod of radius r that passes through the sphere at distance (1/2)R from the center. A string wrapped around the rod pulls with tension T. Find an expression for the sphere's angular acceleration. The rod's moment of inertia is negligible.