Back
BackProblem 15b
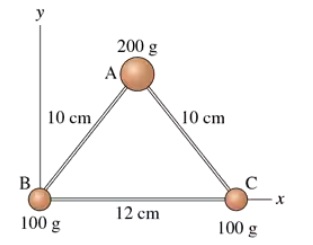
The three masses shown in FIGURE EX12.15 are connected by massless, rigid rods. Find the moment of inertia about an axis that passes through mass A and is perpendicular to the page.
Problem 16a
A 25 kg solid door is 220 cm tall, 91 cm wide. What is the door's moment of inertia for rotation on its hinges?
Problem 16b
A 25 kg solid door is 220 cm tall, 91 cm wide. What is the door’s moment of inertia for rotation about a vertical axis inside the door, 15 cm from one edge?
Problem 17a
A 12-cm-diameter DVD has a mass of 21 g. What is the DVD’s moment of inertia for rotation about a perpendicular axis through its center?
Problem 17b
A 12-cm-diameter DVD has a mass of 21 g. What is the DVD's moment of inertia for rotation about a perpendicular axis through the edge of the disk?
Problem 19
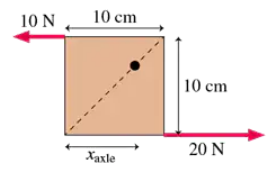
In FIGURE EX12.19, for what value of Xaxle will the two forces provide 1.8 Nm of torque about the axle?
Problem 22
A 4.0-m-long, 500 kg steel beam extends horizontally from the point where it has been bolted to the framework of a new building under construction. A 70 kg construction worker stands at the far end of the beam. What is the magnitude of the torque about the bolt due to the worker and the weight of the beam?
Problem 24
An object's moment of inertia is 2.0 kg m2. Its angular velocity is increasing at the rate of 4.0 rad/s per second. What is the net torque on the object?
Problem 25
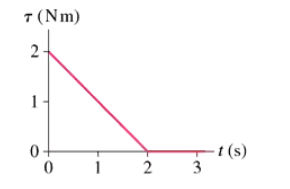
An object whose moment of inertia is 4.0 kg m2 is rotating with angular velocity 0.25 rad/s. It then experiences the torque shown in FIGURE EX12.25. What is the object's angular velocity at t = 3.0s?
Problem 26
A 1.0 kg ball and a 2.0 kg ball are connected by a 1.0-m-long rigid, massless rod. The rod is rotating cw about its center of mass at 20 rpm. What net torque will bring the balls to a halt in 5.0 s?
Problem 27
A 12-cm-diameter, 600 g cylinder, initially at rest, rotates on an axle along its axis. A steady 0.50 N force applied tangent to the edge of the cylinder causes the cylinder to reach an angular velocity of 500 rpm in 2.0 s. What is the magnitude of the frictional torque between the cylinder and the axle?
Problem 29
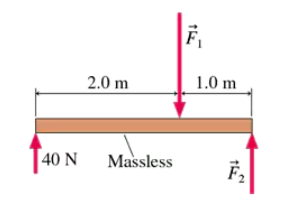
The object shown in FIGURE EX12.29 is in equilibrium. What are the magnitudes of and ?
Problem 32
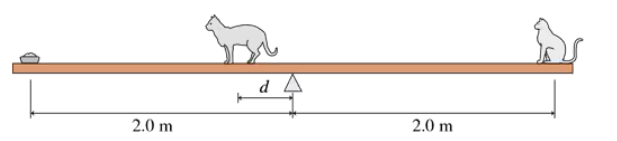
A 5.0 kg cat and a 2.0 kg bowl of tuna fish are at opposite ends of the 4.0-m-long seesaw of FIGURE EX12.32. How far to the left of the pivot must a 4.0 kg cat stand to keep the seesaw balanced?
Problem 33b
A car tire is 60 cm in diameter. The car is traveling at a speed of 20 m/s. What is the speed of a point at the top edge of the tire?
Problem 33c
A car tire is 60 cm in diameter. The car is traveling at a speed of 20 m/s. What is the speed of a point at the bottom edge of the tire?
Problem 34a
An 8.0-cm-diameter, 400 g solid sphere is released from rest at the top of a 2.1-m-long, 25 incline. It rolls, without slipping, to the bottom. What is the sphere’s angular velocity at the bottom of the incline?
Problem 34b
An 8.0-cm-diameter, 400 g solid sphere is released from rest at the top of a 2.1-m-long, 25 incline. It rolls, without slipping, to the bottom. What fraction of its kinetic energy is rotational?
Problem 36
A solid sphere of radius R is placed at a height of 30 cm on a 15° slope. It is released and rolls, without slipping, to the bottom. From what height should a circular hoop of radius R be released on the same slope in order to equal the sphere's speed at the bottom?
Problem 37
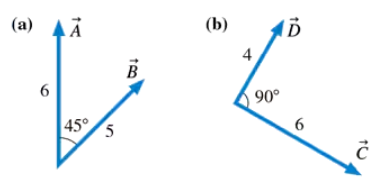
Evaluate the cross products and A ✕ B and C ✕ D.
Problem 39
Vector A = 3î+ĵ and vector B= 3î - 2ĵ + 2k. What is the cross product A ✕ B?
Problem 40
Force is exerted on a particle at . What is the torque on the particle about the origin?
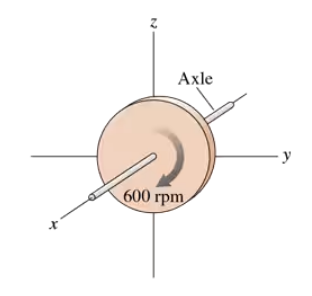
Problem 43
What is the angular momentum vector of the 2.0 kg, 4.0-cm-diameter rotating disk in FIGURE EX12.43? Give your answer using unit vectors.
Problem 44
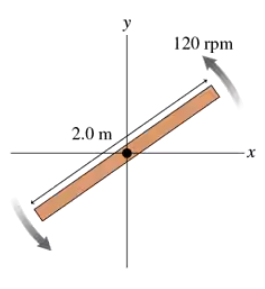
What is the angular momentum vector of the 500 g rotating bar in FIGURE EX12.44? Give your answer using unit vectors.
Problem 45
A 2.0 kg, 20-cm-diameter turntable rotates at 100 rpm on frictionless bearings. Two 500 g blocks fall from above, hit the turntable simultaneously at opposite ends of a diameter, and stick. What is the turntable's angular velocity, in rpm, just after this event?
Problem 47
A 75 g, 6.0-cm-diameter solid spherical top is spun at 1200 rpm on an axle that extends 1.0 cm past the edge of the sphere. The tip of the axle is placed on a support. What is the top's precession frequency in rpm?
Problem 48b
A toy gyroscope has a ring of mass M and radius R attached to the axle by lightweight spokes. The end of the axle is distance R from the center of the ring. The gyroscope is spun at angular velocity ω, then the end of the axle is placed on a support that allows the gyroscope to precess. A 120 g, 8.0-cm-diameter gyroscope is spun at 1000 rpm and allowed to precess. What is the precession period?
Problem 49a
A small 300 g ball and a small 600 g ball are connected by a 40-cm-long, 200 g rigid rod. a. How far is the center of mass from the 600 g ball?
Problem 49b
A small 300 g ball and a small 600 g ball are connected by a 40-cm-long, 200 g rigid rod. b. What is the rotational kinetic energy if the structure rotates about its center of mass at 100 rpm?
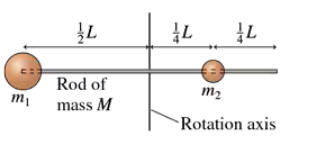
Problem 52
Determine the moment of inertia about the axis of the object shown in FIGURE P12.52.
Problem 53
Calculate by direct integration the moment of inertia for a thin rod of mass M and length L about an axis located distance d from one end. Confirm that your answer agrees with Table 12.2 when d=0 and when d = L/2.