Back
BackProblem 48
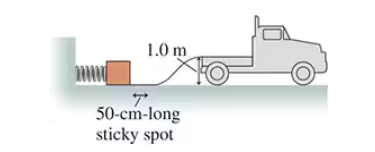
A horizontal spring with spring constant 100 N/m is compressed 20 cm and used to launch a 2.5 kg box across a frictionless, horizontal surface. After the box travels some distance, the surface becomes rough. The coefficient of kinetic friction of the box on the surface is 0.15. Use work and energy to find how far the box slides across the rough surface before stopping.
Problem 49a
Two blocks with masses mA and mB are connected by a massless string over a massless, frictionless pulley. Block B, which is more massive than block A, is released from height h and falls. Write an expression for the speed of the blocks just as block B reaches the ground.
Problem 49b
Two blocks with masses mA and mB are connected by a massless string over a massless, frictionless pulley. Block B, which is more massive than block A, is released from height h and falls. A 1.0 kg block and a 2.0 kg block are connected by a massless string over a massless, frictionless pulley. The impact speed of the heavier block, after falling, is 1.8 m/s. From how high did it fall?
Problem 52a
A freight company uses a compressed spring to shoot 2.0 kg packages up a 1.0-m-high frictionless ramp into a truck, as FIGURE P10.52 shows. The spring constant is 500 N/m and the spring is compressed 30 cm. What is the speed of the package when it reaches the truck?
Problem 53b
The ice cube is replaced by a 50 g plastic cube whose coefficient of kinetic friction is 0.20. How far will the plastic cube travel up the slope? Use work and energy.
Problem 54a
The spring shown in FIGURE P10.54 is compressed 50 cm and used to launch a 100 kg physics student. The track is frictionless until it starts up the incline. The student's coefficient of kinetic friction on the 30° incline is 0.15. What is the student's speed just after losing contact with the spring?
<Image>
Problem 55a
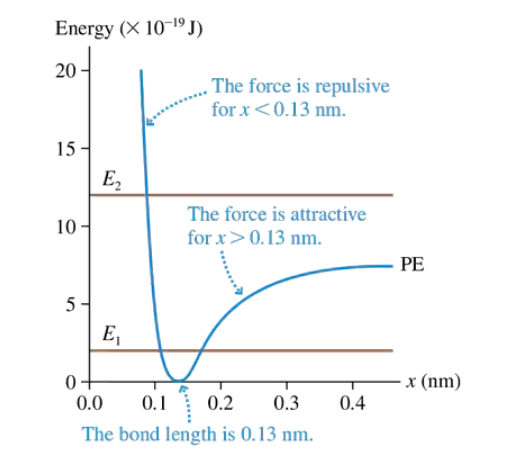
FIGURE 10.23 showed the potential-energy curve for the O2 molecule. Consider a molecule with the energy E1 shown in the figure. a. What is the maximum speed of an oxygen atom as it oscillates back and forth? Don't forget that the kinetic energy is the total kinetic energy of the system. The mass of an oxygen atom is 16 u, where 1 u=1 atomic mass unit =1.66×10−27 kg .
Problem 56a
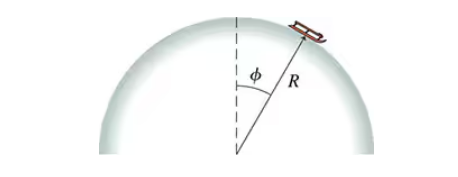
A sled starts from rest at the top of the frictionless, hemispherical, snow-covered hill shown in FIGURE P10.56. a. Find an expression for the sled's speed when it is at angle ϕ .
Problem 57
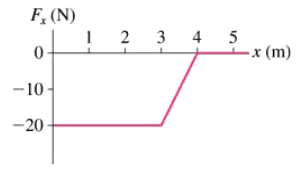
CALC A 2.6 kg block is attached to a horizontal rope that exerts a variable force Fx = (20 − 5x) N, where x is in m. The coefficient of kinetic friction between the block and the floor is 0.25. Initially the block is at rest at x = 0 m. What is the block's speed when it has been pulled to x = 4.0 m?
Problem 58
A 1.0 kg mass that can move along the x-axis experiences the potential energy U = (x²−x) J, where x is in m. The mass has velocity vx = 3.0 m/s at position x = 1.0 m. At what position has it slowed to 1.0 m/s?
Problem 59b
A system has potential energy as a particle moves over the range . For each, is it a point of stable or unstable equilibrium?
Problem 60a
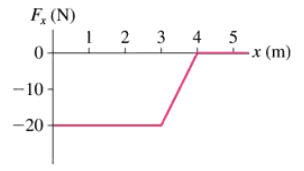
A 100 g particle experiences the one-dimensional, conservative force Fx shown in FIGURE P10.60. Let the zero of potential energy be at x = 0 m . What is the potential energy at x = 1.0, 2.0, 3.0, and 4.0 m? Hint: Use the definition of potential energy and the geometric interpretation of work.
Problem 60b
A 100 g particle experiences the one-dimensional, conservative force Fx shown in FIGURE P10.60. Suppose the particle is shot to the right from x = 1.0 m with a speed of 25 m/s. Where is its turning point?
Problem 61a
A particle that can move along the x-axis is part of a system with potential energy U(x) = A/x2 − B/x where A and B are positive constants. Where are the particle's equilibrium positions?
Problem 62b
A clever engineer designs a 'sprong' that obeys the force law Fx=−q(x−xeq)³ , where xeq is the equilibrium position of the end of the sprong and q is the sprong constant. For simplicity, we'll let xeq = 0 m .Then Fx = −qx³. Find an expression for the potential energy of a stretched or compressed sprong.
Problem 63
CALC The potential energy for a particle that can move along the x-axis is U = Ax2 + B sin(πx/L), where A, B, and L are constants. What is the force on the particle at (a) x = 0, (b) x = L/2, and (c) x = L?
Problem 65a
CALC An object moving in the xy-plane is subjected to the force , where x and y are in m. The particle moves from the origin to the point with coordinates (a, b) by moving first along the x-axis to (a, 0), then parallel to the y-axis. How much work does the force do?
Problem 65c
CALC An object moving in the xy-plane is subjected to the force , where x and y are in m. Is this a conservative force?
Problem 71
In a physics lab experiment, a compressed spring launches a 20 g metal ball at a 30° angle. Compressing the spring 20 cm causes the ball to hit the floor 1.5 m below the point at which it leaves the spring after traveling 5.0 m horizontally. What is the spring constant?
Problem 73a
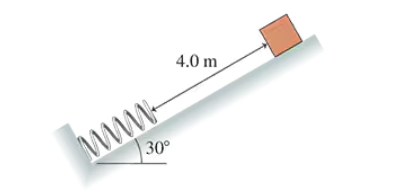
A 10 kg box slides 4.0 m down the frictionless ramp shown in FIGURE CP10.73, then collides with a spring whose spring constant is 250 N/m. What is the maximum compression of the spring?