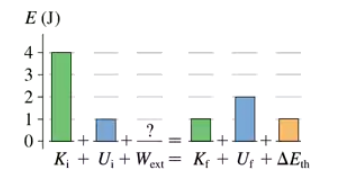Back
BackProblem 1a
A system of two objects has and . How much work is done by interaction forces?
Problem 2
A system consists of interacting objects A and B, each exerting a constant 3.0 N pull on the other. What is ∆U for the system if A moves 1.0 m toward B while B moves 2.0 m toward A?
Problem 4
The free-fall acceleration on a large asteroid, in the vacuum of space, is 0.15 m/s2. A spacecraft hovering 500 m above the surface drops a 25 kg payload wrapped in a padded jacket. What is the payload's impact speed?
Problem 6
A 55 kg skateboarder wants to just make it to the upper edge of a 'quarter pipe,' a track that is one-quarter of a circle with a radius of 3.0 m. What speed does he need at the bottom?
Problem 9
A 20 kg child is on a swing that hangs from 3.0-m-long chains. What is her maximum speed if she swings out to a 45° angle?
- The spring in FIGURE EX10.21a is compressed by 10 cm. It launches a block across a frictionless surface at 0.50 m/s. The two springs in Figure EX10.21b are identical to the spring of Figure EX10.21a. They are compressed by the same 10 cm and launch the same block. What is the block's speed now?
Problem 10
Problem 10a
A pendulum is made by tying a 500 g ball to a 75-cm-long string. The pendulum is pulled 30° to one side, then released. What is the ball's speed at the lowest point of its trajectory?
Problem 11
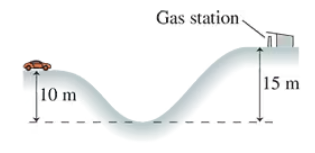
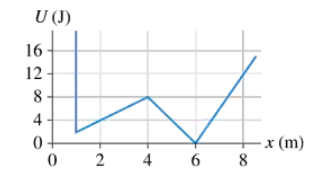
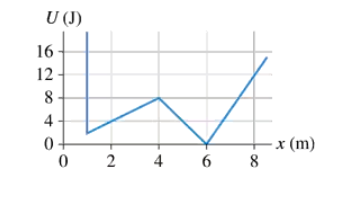
A 1500 kg car traveling at 10 m/s suddenly runs out of gas while approaching the valley shown in FIGURE EX10.11. The alert driver immediately puts the car in neutral so that it will roll. What will be the car's speed as it coasts into the gas station on the other side of the valley? Ignore rolling friction.
Problem 12
The maximum energy a bone can absorb without breaking is surprisingly small. Experimental data show that a leg bone of a healthy, 60 kg human can absorb about 200 J. From what maximum height could a 60 kg person jump and land rigidly upright on both feet without breaking his legs? Assume that all energy is absorbed by the leg bones in a rigid landing.
Problem 14a
In a hydroelectric dam, water falls 25 m and then spins a turbine to generate electricity. What is of 1.0 kg of water?
Problem 14b
In a hydroelectric dam, water falls 25 m and then spins a turbine to generate electricity. Suppose the dam is 80% efficient at converting the water's potential energy to electrical energy. How many kilograms of water must pass through the turbines each second to generate 50 MW of electricity? This is a typical value for a small hydroelectric dam.
Problem 17
A stretched spring stores 2.0 J of energy. How much energy will be stored if the spring is stretched three times as far?
Problem 19
As a 15,000 kg jet plane lands on an aircraft carrier, its tail hook snags a cable to slow it down. The cable is attached to a spring with spring constant 60,000 N/m. If the spring stretches 30 m to stop the plane, what was the plane's landing speed?
Problem 23
The elastic energy stored in your tendons can contribute up to 35% of your energy needs when running. Sports scientists find that (on average) the knee extensor tendons in sprinters stretch 41 mm while those of nonathletes stretch only 33 mm. The spring constant of the tendon is the same for both groups, 33 N/mm. What is the difference in maximum stored energy between the sprinters and the nonathletes?
Problem 24
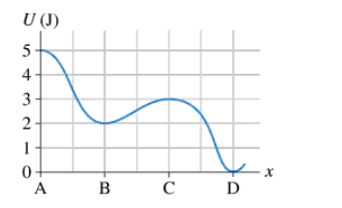
FIGURE EX10.24 is the potential-energy diagram for a 500 g particle that is released from rest at A. What are the particle's speeds at B, C, and D?
Problem 25b
FIGURE EX10.25 is the potential-energy diagram for a 20 g particle that is released from rest at x = 1.0 m. What is the particle's maximum speed? At what position does it have this speed?
Problem 26b
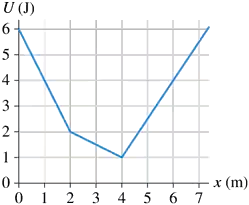
In FIGURE EX10.26, What minimum speed does a 100 g particle need at point B to reach point A?
Problem 27
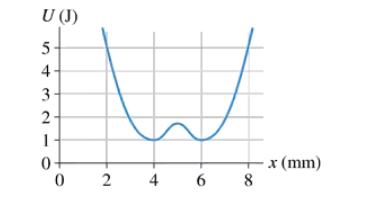
In FIGURE EX10.27, what is the maximum speed of a 2.0 g particle that oscillates between x = 2.0 mm and x = 8.0 mm
Problem 28a
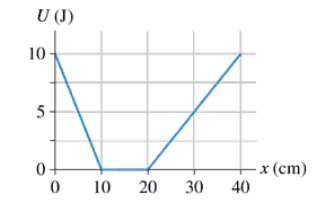
FIGURE EX10.28 shows the potential-energy diagram for a 500 g particle as it moves along the x-axis. Suppose the particle's mechanical energy is 12 J. Where are the particle's turning points?
Problem 29
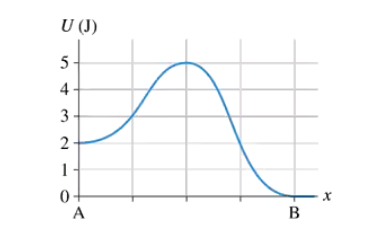
In FIGURE EX10.28, what is the maximum speed a 200 g particle could have at x = 2.0 m and never reach x = 6.0 m?
Problem 31
A system in which only one particle moves has the potential energy shown in FIGURE EX10.31. What is the x-component of the force on the particle at x = 5, 15, and 25 cm?
Problem 32
A particle moving along the y-axis is in a system with potential energy U = 4y3 J, where y is in m. What is the y-component of the force on the particle at y = 0 m, 1 m, and 2 m?
Problem 34b
A particle moving along the x-axis is in a system that has potential energy U = x3 - 3x J, where x is in m. For each, is it a point of stable or unstable equilibrium?
Problem 36b
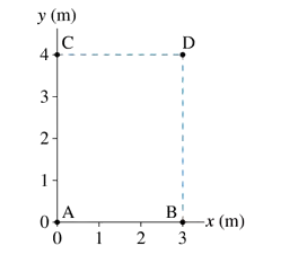
A particle moves from A to D in FIGURE EX10.36 while experiencing force F = (6i + 8j) N. How much work does the force do if the particle follows path ACD. Is this a conservative force? Explain.
Problem 39
How much work is done by the environment in the process shown in FIGURE EX10.39? Is energy transferred from the environment to the system or from the system to the environment?
Problem 40
A cable with 20.0 N of tension pulls straight up on a 1.50 kg block that is initially at rest. What is the block's speed after being lifted 2.00 m? Solve this problem using work and energy.
Problem 41
A 50 g mass is attached to a light, rigid, 75-cm-long rod. The other end of the rod is pivoted so that the mass can rotate in a vertical circle. What speed does the mass need at the bottom of the circle to barely make it over the top of the circle?
Problem 42
A 50 g ice cube can slide up and down a frictionless 30° slope. At the bottom, a spring with spring constant 25 N/m is compressed 10 cm and used to launch the ice cube up the slope. How high does it go above its starting point?
Problem 43b
You have been hired to design a spring-launched roller coaster that will carry two passengers per car. The car goes up a 10-m-high hill, then descends 15 m to the track's lowest point. You've determined that the spring can be compressed a maximum of 2.0 m and that a loaded car will have a maximum mass of 400 kg. For safety reasons, the spring constant should be 10% larger than the minimum needed for the car to just make it over the top. What is the maximum speed of a 350 kg car if the spring is compressed the full amount?
Problem 44
A block of mass m slides down a frictionless track, then around the inside of a circular loop-the-loop of radius R . From what minimum height h must the block start to make it around without falling off? Give your answer as a multiple of R.