A ball shot straight up with kinetic energy K₀ reaches height h. What height will it reach if the initial kinetic energy is doubled?

A 50 kg ice skater is gliding along the ice, heading due north at 4.0 m/s. The ice has a small coefficient of static friction, to prevent the skater from slipping sideways, but μ_k = 0. Suddenly, a wind from the northeast exerts a force of 4.0 N on the skater. Use work and energy to find the skater's speed after gliding 100 m in this wind.

A 50 kg ice skater is gliding along the ice, heading due north at 4.0 m/s. The ice has a small coefficient of static friction, to prevent the skater from slipping sideways, but μ_k = 0. Suddenly, a wind from the northeast exerts a force of 4.0 N on the skater. What is the minimum value of μ_s that allows her to continue moving straight north?

A 737-800 jet airliner has twin engines, each with 105 kN thrust. A 78,000 kg jet reaches a takeoff speed of 70 m/s in a distance of 1100 m. What is the increase in thermal energy due to rolling friction and air drag?

The gravitational attraction between two objects with masses m_A and m_B, separated by distance 𝓍, is F = Gm_Am_B/𝓍², where G is the gravitational constant. If one mass is much greater than the other, the larger mass stays essentially at rest while the smaller mass moves toward it. Suppose a 1.5 x 10¹³ kg comet is passing the orbit of Mars, heading straight for the sun at a speed of 3.5 x 10⁴ m/s. What will its speed be when it crosses the orbit of Mercury? Astronomical data are given in the tables at the back of the book, and G = 6.67 x 10^-11 Nm²/kg².

A red ball has a mass of 250 g. A constant force pushes the red ball horizontally and launches it at a speed of 15 m/s. The same force pushes a green ball through the same distance, launching it at 25 m/s. What is the mass of the green ball?

A 30 g mass is attached to one end of a 10-cm-long spring. The other end of the spring is connected to a frictionless pivot on a frictionless, horizontal surface. Spinning the mass around in a circle at 90 rpm causes the spring to stretch to a length of 12 cm. What is the value of the spring constant?

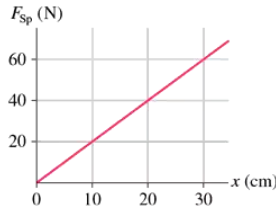
A 50 g rock is placed in a slingshot and the rubber band is stretched. The magnitude of the force of the rubber band on the rock is shown by the graph in FIGURE P9.56. The rubber band is stretched 30 cm and then released. What is the speed of the rock?

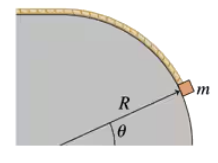
How much work does tension do to pull the mass from the bottom of the hill (θ = 0) to the top at constant speed? To answer this question, write an expression for the work done when the mass moves through a very small distance ds while it has angle θ, replace ds with an equivalent expression involving R and dθ, then integrate.

A horizontal spring with spring constant 250 N/m is compressed by 12 cm and then used to launch a 250 g box across the floor. The coefficient of kinetic friction between the box and the floor is 0.23. What is the box's launch speed?

A spring of equilibrium length L₁ and spring constant k₁ hangs from the ceiling. Mass m₁ is suspended from its lower end. Then a second spring, with equilibrium length L₂ and spring constant k₂, is hung from the bottom of m₁. Mass m₂ is suspended from this second spring. How far is m₂ below the ceiling?

A 90 kg firefighter needs to climb the stairs of a 20-m-tall building while carrying a 40 kg backpack filled with gear. How much power does he need to reach the top in 55 s?

A hydroelectric power plant uses spinning turbines to transform the kinetic energy of moving water into electric energy with 80% efficiency. That is, 80% of the kinetic energy becomes electric energy. A small hydroelectric plant at the base of a dam generates 50 MW of electric power when the falling water has a speed of 18 m/s. What is the water flow rate - kilograms of water per second - through the turbines?

When you ride a bicycle at constant speed, nearly all the energy you expend goes into the work you do against the drag force of the air. Model a cyclist as having cross-section area 0.45 m² and, because the human body is not aerodynamically shaped, a drag coefficient of 0.90. Use 1.2 kg/m³ as the density of air at room temperature. Metabolic power is the rate at which your body 'burns' fuel to power your activities. For many activities, your body is roughly 25% efficient at converting the chemical energy of food into mechanical energy. What is the cyclist's metabolic power while cycling at 7.3 m/s?

When you ride a bicycle at constant speed, nearly all the energy you expend goes into the work you do against the drag force of the air. Model a cyclist as having cross-section area 0.45 m² and, because the human body is not aerodynamically shaped, a drag coefficient of 0.90. Use 1.2 kg/m³ as the density of air at room temperature. The food calorie is equivalent to 4190 J. How many calories does the cyclist burn if he rides over level ground at 7.3 m/s for 1 h?

A Porsche 944 Turbo has a rated engine power of 217 hp. 30% of the power is lost in the engine and the drive train, and 70% reaches the wheels. The total mass of the car and driver is 1480 kg, and two-thirds of the weight is over the drive wheels. What is the maximum acceleration of the Porsche on a concrete surface where μ_s = 1.00? Hint: What force pushes the car forward?

A Porsche 944 Turbo has a rated engine power of 217 hp. 30% of the power is lost in the engine and the drive train, and 70% reaches the wheels. The total mass of the car and driver is 1480 kg, and two-thirds of the weight is over the drive wheels. If the Porsche accelerates at a_max, what is its speed when it reaches maximum power output?

A Porsche 944 Turbo has a rated engine power of 217 hp. 30% of the power is lost in the engine and the drive train, and 70% reaches the wheels. The total mass of the car and driver is 1480 kg, and two-thirds of the weight is over the drive wheels. How long does it take the Porsche to reach the maximum power output?

A farmer uses a tractor to pull a 150 kg bale of hay up a 15° incline to the barn at a steady 5.0 km/h. The coefficient of kinetic friction between the bale and the ramp is 0.45. What is the tractor's power output?

Astronomers using a 2.0-m-diameter telescope observe a distant supernova - an exploding star. The telescope's detector records 9.1 x 10^-11 J of light energy during the first 10 s. It's known that this type of supernova has a visible-light power output of 5.0 x 10³⁷ W for the first 10 s of the explosion. How distant is the supernova? Give your answer in light years, where one light year is the distance light travels in one year. The speed of light is 3.0 x 10⁸ m/s.

Write a realistic problem for which this is the correct equation(s).

$T-\left(1500\text{kg}\right)\left(9.8{\text{m/s}}^2\right)=\left(1500\text{kg}\right)\left(1.0{\text{m/s}}^2\right)$

$P=T\left(2.0\text{m/s}\right)$

Draw a pictorial representation.

$T-(1500\,\text{kg})(9.8\,\text{m/s}^2)=(1500\,\text{kg})\left(1.0\,\text{m/s}^2\right)$

$P=T(2.0\,\text{m/s})$

Finish the solution of the problem.

$T-(1500\,\text{kg})(9.8\,\text{m/s}^2)=(1500\,\text{kg})\left(1.0\,\text{m/s}^2\right)$

$P=T(2.0\,\text{m/s})$

A 12 kg weather rocket generates a thrust of 200 N. The rocket, pointing upward, is clamped to the top of a vertical spring. The bottom of the spring, whose spring constant is 550 N/m, is anchored to the ground. Initially, before the engine is ignited, the rocket sits at rest on top of the spring. How much is the spring compressed?

A 12 kg weather rocket generates a thrust of 200 N. The rocket, pointing upward, is clamped to the top of a vertical spring. The bottom of the spring, whose spring constant is 550 N/m, is anchored to the ground. After the engine is ignited, what is the rocket’s speed when the spring has stretched 40 cm?

A gardener pushes a 12 kg lawnmower whose handle is tilted up 37° above horizontal. The lawnmower's coefficient of rolling friction is 0.15. How much power does the gardener have to supply to push the lawnmower at a constant speed of 1.2 m/s? Assume his push is parallel to the handle.